揭秘:拐点究竟是几何点还是坐标系中的秘密坐标?
拐点:一个几何与代数交织的概念辨析

在数学的广阔天地里,拐点是一个既常见又充满争议的概念。它既是几何图形上的一个显著特征点,又常常与坐标系统中的数值紧密相连。那么,拐点究竟是点还是坐标呢?为了全面而深入地解答这一问题,我们需要从多个角度进行剖析。

首先,我们需要明确“拐点”这一术语在数学中的基本定义。拐点,又称为反曲点,是曲线上一个点,该点两侧的切线斜率符号相反,即曲线在这一点由凸变凹或由凹变凸。从这个定义出发,我们可以初步判断拐点首先是几何图形上的一个具体点。然而,当我们将这一几何概念引入坐标系统时,拐点的描述便不可避免地与坐标值产生了关联。

在平面直角坐标系中,每一个点都可以通过一对有序实数(即坐标)来唯一确定。拐点作为曲线上的一个特殊点,也不例外。当我们需要精确描述拐点在曲线上的位置时,通常会给出其对应的坐标值。这时,拐点在代数层面上的表现便是一组特定的坐标。
但值得注意的是,坐标只是对拐点位置的一种量化描述方式,它并不改变拐点作为几何图形上点的本质属性。换句话说,坐标是拐点的“语言”,是我们为了交流和计算而赋予拐点的一种数学表示。离开了坐标系统,拐点仍然是一个几何实体,只不过我们无法用数值来精确描述它的位置。
为了更直观地理解拐点与坐标的关系,我们可以借助具体的数学例子进行说明。例如,考虑二次函数y=ax^2+bx+c的图像——一条抛物线。对于这条抛物线,我们可以通过求导找到其拐点(如果存在的话)。设y'=2ax+b,令y'=0,解得x=-b/(2a)。将x=-b/(2a)代入原函数y=ax^2+bx+c,即可求得对应的y值。这样,我们就得到了拐点的坐标(-b/(2a), c-b^2/(4a))。
在这个例子中,拐点是抛物线上一个具体的点,它的位置由抛物线的方程决定。而坐标(-b/(2a), c-b^2/(4a))则是我们在坐标系统中用来描述这一点的工具。两者相辅相成,共同构成了对拐点这一概念的完整描述。
然而,在实际应用中,我们有时会遇到一些容易混淆的情况。例如,在某些数学或物理问题中,我们可能会遇到“求拐点”这样的表述。这时,我们的任务通常是找到拐点的坐标值,因为只有这样我们才能用数值的方式精确地描述拐点的位置。但在这个过程中,我们不应该忘记拐点作为几何图形上点的本质属性。
此外,还有一些特殊情况需要我们注意。在某些曲线中,拐点可能不存在或者不止一个。例如,对于一条直线来说,由于其斜率在整个定义域内都是常数,因此不存在拐点。而对于某些复杂的曲线来说,可能存在多个拐点。这时,我们就需要利用更高级的数学工具(如微积分中的导数)来找到这些拐点,并分别求出它们的坐标值。
除了平面直角坐标系外,拐点在其他类型的坐标系(如极坐标系、三维直角坐标系等)中同样存在。在这些坐标系中,拐点的描述方式可能会有所不同,但其作为几何图形上点的本质属性仍然保持不变。同时,随着坐标系的变换,拐点的坐标值也会相应地发生变化。这进一步证明了坐标只是对拐点位置的一种描述方式,而不是拐点本身。
综上所述,拐点既是几何图形上的一个具体点,又可以通过坐标系统中的数值进行描述。两者之间的关系是密切而微妙的。拐点作为几何实体,其位置由曲线的方程决定;而坐标则是对这一位置进行量化描述的工具。在实际应用中,我们需要根据问题的具体需求来选择使用哪种描述方式。但无论采用哪种方式,我们都不应该忘记拐点作为几何图形上点的本质属性。
最后,需要强调的是,拐点这一概念在数学和物理学等多个领域都有着广泛的应用。在数学中,拐点是微积分和微分方程等重要分支的研究对象之一;在物理学中,拐点则常常与物理过程的极值点和转折点相对应。因此,深入理解和掌握拐点的概念对于提高我们的数学素养和解决实际问题具有重要意义。
总之,拐点既是点也是坐标的说法并不矛盾。它是几何与代数交织的产物,既具有几何图形的直观性又具有代数的精确性。通过全面而深入地理解拐点的概念及其与坐标的关系,我们可以更好地把握数学和物理学中的相关规律和方法,为解决实际问题提供有力的数学支持。
- 上一篇: 夏有乔木 雅望天堂:电影版震撼结局揭秘
- 下一篇: 揭秘:KISS的真正含义是什么?
-
 绝对值最小的数是什么?资讯攻略02-28
绝对值最小的数是什么?资讯攻略02-28 -
 QQ三国4月12日逃犯坐标查询方法揭秘资讯攻略02-16
QQ三国4月12日逃犯坐标查询方法揭秘资讯攻略02-16 -
 揭秘:乌克兰在全球版图的独特坐标!资讯攻略02-24
揭秘:乌克兰在全球版图的独特坐标!资讯攻略02-24 -
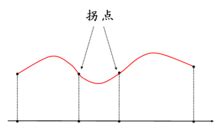 拐点的定义与解析资讯攻略05-02
拐点的定义与解析资讯攻略05-02 -
 探寻四川省四川师范大学文理学院金堂校区的神秘坐标资讯攻略01-22
探寻四川省四川师范大学文理学院金堂校区的神秘坐标资讯攻略01-22 -
 揭秘:开盘价到底是什么?资讯攻略04-08
揭秘:开盘价到底是什么?资讯攻略04-08












