2020高考数学“金字塔”题目最优解法探究
在探讨2020年高考数学中备受瞩目的“金字塔”题目的最佳解法时,我们首先需要明确该题目的具体内容和要求。这道题目以其独特的几何形状和复杂的计算逻辑,成为了当年考生们热议的焦点。题目要求考生在给定的金字塔几何模型中,通过精确的数学计算,求解出与金字塔相关的一系列参数或性质。

首先,我们回顾一下题目的基本设定。一个典型的金字塔形状,底部为正方形,顶点垂直于底面中心。题目可能涉及到金字塔的高、底边长、斜边长等参数的求解,或者要求计算金字塔的体积、表面积等几何量。为了找到最佳解法,我们需要综合运用立体几何、三角函数、代数运算等数学知识。

在解题过程中,第一步是仔细审题,明确题目所求。对于涉及金字塔体积的问题,我们可以利用立体几何中的体积公式V=1/3*S*h,其中S为底面积,h为高。若题目给出了金字塔的底面边长a和高h,则底面积S=a²,体积V即可轻松求出。若题目未直接给出高h,而是通过其他条件间接给出,则需要我们利用勾股定理或三角函数等工具先求出高h。

对于涉及金字塔表面积的问题,我们需要知道金字塔的表面积由底面和四个侧面组成。底面面积为a²,每个侧面的面积可以通过斜边b和与之相邻的底面边长所构成的直角三角形来计算,即侧面面积=1/2*a*b。因此,总表面积S总=a²+4*(1/2*a*b)=a²+2ab。同样,若斜边b未直接给出,则需要我们通过其他条件先求出b。

接下来,我们以一个具体的“金字塔”题目为例,来展示最佳解法的应用。假设题目要求求解一个底面边长为4、斜边长为5的金字塔的体积。首先,我们根据勾股定理求出金字塔的高h。设金字塔的高为h,底面中心到顶点的距离为斜边b(此处b已知为5),底面边长的一半为a/2(此处a/2=2)。根据勾股定理,有h²+(a/2)²=b²,代入已知数值解得h²+4=25,进而求得h=√21。
有了高h,我们就可以利用体积公式求出金字塔的体积。将S=a²=16和h=√21代入体积公式V=1/3*S*h,得到V=1/3*16*√21=16√21/3。这就是该金字塔的体积的最佳解法。
若题目要求求解的是金字塔的表面积,我们同样可以利用已知的底面边长a和斜边长b来求解。将a=4和b=5代入表面积公式S总=a²+2ab,得到S总=16+2*4*5=16+40=56。这就是该金字塔的表面积的最佳解法。
在解题过程中,我们还需要注意一些常见的陷阱和误区。例如,有些考生可能会忽略题目中的单位换算,导致计算结果出错。还有些考生可能会在计算过程中出现粗心大意的情况,如算错平方根、忘记乘以或除以某个系数等。因此,在解题时我们需要保持冷静、细心审题、仔细计算,以确保解题过程的准确性和完整性。
此外,对于一些较为复杂的“金字塔”题目,我们可能需要综合运用多种数学知识和技巧来求解。例如,有些题目可能会涉及到空间向量的应用、球坐标与直角坐标的转换等高级数学知识。对于这类题目,我们需要先对题目进行深入的剖析和理解,再选择合适的数学工具和方法进行求解。
在备考过程中,我们可以通过多做练习题来加深对“金字塔”题目及其解法的理解和掌握。通过不断的练习和实践,我们可以提高自己的解题速度和准确率,从而在高考中取得更好的成绩。
同时,我们还需要注意保持良好的学习态度和心态。高考是一场重要的考试,但它并不是衡量我们人生价值的唯一标准。因此,在备考过程中我们需要保持积极、乐观的心态,相信自己能够克服困难、取得优异的成绩。即使遇到挫折和困难也不要气馁和放弃,而是要坚持到底、勇往直前。
综上所述,对于2020年高考数学中的“金字塔”题目,我们可以通过仔细审题、明确题目所求、综合运用数学知识和方法、注意陷阱和误区等方式来找到最佳解法。同时,我们还需要通过多做练习题来加深对题目的理解和掌握,并保持良好的学习态度和心态来迎接高考的挑战。相信只要我们付出足够的努力和汗水,就一定能够在高考中取得优异的成绩。
- 上一篇: 羽毛球通常包含多少根羽毛?
- 下一篇: 苹果手机如何自带水印功能?
-
 2020年高考揭秘:语文作文题目究竟是什么?资讯攻略02-09
2020年高考揭秘:语文作文题目究竟是什么?资讯攻略02-09 -
 2022年高考数学I卷:深度剖析试题精髓与解题策略资讯攻略01-26
2022年高考数学I卷:深度剖析试题精髓与解题策略资讯攻略01-26 -
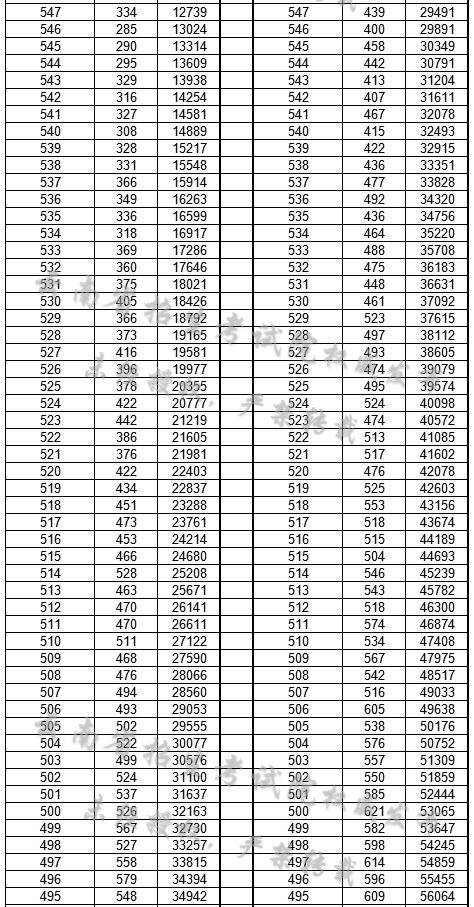 揭秘!2020年高考总分大揭秘资讯攻略01-05
揭秘!2020年高考总分大揭秘资讯攻略01-05 -
 揭秘!今年高考作文题目大猜想资讯攻略01-17
揭秘!今年高考作文题目大猜想资讯攻略01-17 -
 埃及胡夫金字塔的高度相当于多少层大楼?资讯攻略03-21
埃及胡夫金字塔的高度相当于多少层大楼?资讯攻略03-21 -
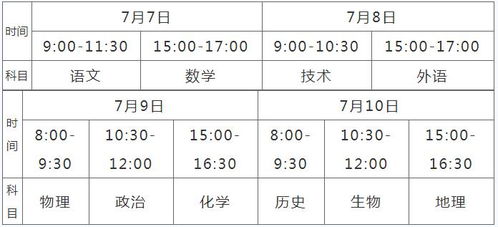 2020年高考具体是在哪一天?资讯攻略01-17
2020年高考具体是在哪一天?资讯攻略01-17












