极化恒等式的定义是什么?
极化恒等式是数学中一个重要的等式,尤其在三角函数和向量运算中有着广泛的应用。为了深入理解极化恒等式,我们可以从多个角度进行探讨,并展示其在不同情境下的具体应用。

在数学领域中,极化恒等式是连接三角函数和向量运算的一座桥梁。简而言之,极化恒等式揭示了向量点积和叉积与三角函数之间的关系。具体来说,如果我们有两个向量a和b,以及它们的夹角θ,那么向量a和b的点积可以表示为|a|·|b|·cosθ,向量a和b的叉积的模可以表示为|a|·|b|·sinθ。这两个表达式构成了极化恒等式的基础,将向量的几何意义与三角函数的代数形式紧密地联系在一起。
从三角函数的角度来看,极化恒等式具有简洁性和普遍性。在平面直角坐标系中,任意一个角θ的正弦、余弦和正切值都可以通过单位圆上的点来定义。极化恒等式则进一步揭示了这些三角函数值之间的内在联系。例如,我们可以利用极化恒等式将sin(a+b)和cos(a+b)展开为sin a、cos a、sin b和cos b的函数,从而得到两角和的正弦和余弦公式。这些公式不仅在数学内部有着广泛的应用,如求解三角函数的值、化简三角表达式等,而且在物理、工程等领域也具有重要价值。
在向量运算中,极化恒等式同样发挥着重要作用。向量作为数学和物理学中的一个基本概念,具有大小和方向两个属性。极化恒等式将向量的点积和叉积与夹角θ联系起来,从而揭示了向量之间的相互作用关系。例如,在物理学中,力、速度和加速度等物理量都是向量,它们之间的相互作用关系往往可以通过极化恒等式来描述。此外,在图形学和计算机视觉等领域中,极化恒等式也被广泛应用于计算图形的面积、体积以及求解向量之间的夹角等问题。
除了在三角函数和向量运算中的应用外,极化恒等式还在数学的其他分支中发挥着重要作用。例如,在复变函数中,极化恒等式可以用于描述复数的模和辐角之间的关系。在解析几何中,极化恒等式可以用于求解直线和圆等几何图形之间的位置关系。在微积分中,极化恒等式则可以用于计算曲线和曲面的面积、体积等几何量。这些应用不仅展示了极化恒等式的广泛性和实用性,也进一步证明了数学内部各个分支之间的紧密联系和相互渗透。
此外,极化恒等式还具有一些独特的性质和特点。首先,它具有对称性。在极化恒等式中,向量a和b的地位是平等的,无论我们先考虑哪个向量都不会影响最终的结果。这种对称性使得极化恒等式在应用中更加灵活和方便。其次,极化恒等式具有可加性。即当我们有多个向量时,可以利用极化恒等式将它们之间的相互作用关系进行叠加和分解。这种可加性为处理复杂问题提供了有力的数学工具。最后,极化恒等式还具有普适性。无论是在二维平面还是三维空间中,无论是在静态还是动态情况下,极化恒等式都可以为我们提供有效的数学描述和计算方法。
为了深入理解极化恒等式的本质和内涵,我们可以尝试通过一些具体的例子来进行说明。例如,在物理学中,当两个力F1和F2作用于同一个物体时,它们之间的合力F可以通过极化恒等式来计算。具体来说,我们可以将F1和F2分别表示为向量形式,并计算它们之间的夹角θ。然后利用极化恒等式将F1和F2的点积和叉积表示为它们的大小和夹角θ的函数。最后通过求解这些函数来得到合力F的大小和方向。这个例子不仅展示了极化恒等式在物理学中的应用价值,也为我们提供了一种有效的数学方法来处理复杂的物理问题。
另一个例子是在图形学中计算多边形的面积。对于一个由n个顶点构成的平面多边形,我们可以将其划分为n-2个三角形,并分别计算每个三角形的面积。然后利用极化恒等式将每个三角形的面积表示为其顶点坐标的函数,并通过求解这些函数来得到多边形的总面积。这种方法不仅具有精确性和高效性,还可以避免传统的面积计算方法中出现的误差和冗余。
综上所述,极化恒等式是数学中一个重要的等式,在三角函数、向量运算以及其他数学分支中都有着广泛的应用。通过深入理解极化恒等式的本质和内涵,我们可以更好地掌握数学的基本概念和原理,为解决复杂问题提供有力的数学工具和方法。同时,我们也可以将极化恒等式应用于实际问题的求解中,从而推动数学在各个领域中的发展和应用。在未来的学习和研究中,我们应该继续深入挖掘极化恒等式的潜在价值和应用前景,为推动数学和科学技术的进步做出更大的贡献。
- 上一篇: What Does 'Amusing' Mean?
- 下一篇: 揭秘:“一只”的拼音拼读奥秘!
-
 探究1+1为何等于2资讯攻略03-30
探究1+1为何等于2资讯攻略03-30 -
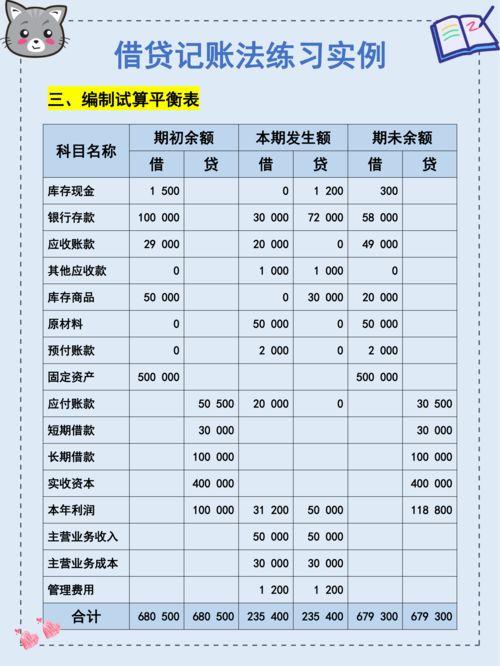 什么是借贷记账法?资讯攻略04-24
什么是借贷记账法?资讯攻略04-24 -
 探究'等量齐观'的深层含义:平等视角下的比较与审视资讯攻略03-27
探究'等量齐观'的深层含义:平等视角下的比较与审视资讯攻略03-27 -
 卡片相机的定义是什么?资讯攻略03-08
卡片相机的定义是什么?资讯攻略03-08 -
 辛勤劳动的定义是什么?资讯攻略03-28
辛勤劳动的定义是什么?资讯攻略03-28 -
 俗人的定义是什么?资讯攻略02-19
俗人的定义是什么?资讯攻略02-19