揭秘：力矩的单位究竟是什么？

力矩的单位深度解析

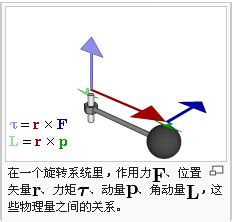
在物理学和工程学中，力矩是一个至关重要的概念，它描述了力的旋转效果。要深入理解力矩，我们首先需要明确其单位，这是衡量力矩大小的基础。本文将从力矩的定义、计算公式、单位推导、实际应用以及与其他物理量的关系等多个维度，对力矩的单位进行深度解析。

一、力矩的定义与计算公式

力矩，简单来说，就是力和力臂的乘积，它衡量了一个力使物体绕某点旋转的效果。在数学表达式中，力矩M通常由以下公式给出：

M = F × d

其中，F代表作用在物体上的力，d是从旋转轴（或参考点）到力的作用线的垂直距离，即力臂。这个公式清晰地表明了力矩与力和力臂之间的直接关系。

二、力矩的单位推导

为了确定力矩的单位，我们需要先了解力和力臂的单位。在国际单位制（SI）中，力的单位是牛顿（N），而距离（力臂）的单位是米（m）。根据力矩的计算公式M = F × d，我们可以推导出力矩的单位：

M的单位 = N的单位 × m的单位 = 牛顿·米（N·m）

因此，力矩的单位是牛顿·米，这是一个复合单位，表示了力和距离的乘积所产生的旋转效果。

三、力矩单位的实际应用

在实际应用中，力矩单位的理解和运用至关重要。例如，在机械设计中，工程师需要计算传动轴或齿轮的力矩，以确保机械系统的正常运行。在这些情况下，力矩的大小直接关系到系统的负载能力和效率。使用牛顿·米作为单位，可以精确地描述和比较不同设计方案的力矩性能。

此外，在物理学和工程学的教学和研究中，力矩单位也是不可或缺的一部分。学生们在学习力学和动力学时，需要掌握力矩的概念和计算方法，以及如何在不同情境下应用力矩单位。研究人员则在进行力学实验和模拟时，依赖力矩单位来量化和分析实验结果。

四、力矩与其他物理量的关系

力矩不仅与力和力臂直接相关，还与角动量、角速度和扭矩等物理量密切相关。

1. 角动量

角动量是描述物体绕某点旋转时具有的动量。它与力矩的关系可以通过角动量定理来表达：物体角动量的变化率等于作用在物体上的合外力矩。这意味着，当一个物体受到力矩作用时，它的角动量会发生变化。在SI单位制中，角动量的单位是千克·平方米/秒（kg·m²/s），这反映了它与质量、距离和时间的关系。

2. 角速度

角速度是描述物体绕某点旋转的快慢程度的物理量。虽然角速度本身与力矩没有直接关系，但力矩可以影响物体的角加速度，进而通过积分影响角速度。在SI单位制中，角速度的单位是弧度/秒（rad/s）。

3. 扭矩

扭矩是力矩的一种特殊形式，它特指作用在旋转轴上、使轴产生扭转效果的力矩。在机械工程中，扭矩是衡量轴或螺栓等连接件受力情况的重要指标。扭矩的单位也是牛顿·米（N·m），这与一般力矩的单位相同。

五、力矩单位的转换与标准化

在不同的物理和工程领域，可能会遇到其他表示力矩的单位。例如，在某些情况下，可能会使用磅力·英尺（lbf·ft）作为力矩的单位。这种单位是基于英制单位系统（IPS）的，与SI单位制中的牛顿·米有所不同。为了进行跨领域的比较和分析，通常需要将力矩单位进行转换。例如，1磅力·英尺大约等于1.35582牛顿·米。

随着国际单位制的普及和标准化进程的推进，越来越多的领域开始采用SI单位制来表示力矩。这有助于减少因单位不同而导致的误解和错误，促进不同领域之间的交流和合作。

六、力矩单位在教育和科研中的应用

在教育和科研领域，力矩单位的应用同样广泛而重要。在教育方面，学生们在学习力学和动力学课程时，需要掌握力矩的概念、计算公式和单位。这有助于他们理解物体旋转的基本原理和规律，为后续的专业学习和实践打下坚实的基础。在科研方面，研究人员在进行力学实验和模拟时，依赖力矩单位来量化和分析实验结果。这有助于他们揭示物体旋转的内在机制和规律，推动力学学科的发展和创新。

七、结论

综上所述，力矩的单位是牛顿·米，这一单位基于力矩的定义和计算公式推导得出。在实际应用中，力矩单位在机械设计、物理学和工程学的教学与研究以及跨领域的比较和分析中发挥着重要作用。同时，力矩单位与角动量、角速度和扭矩等物理量密切相关，这进一步丰富了我们对力矩单位的理解和运用。随着国际单位制的普及和标准化进程的推进，力矩单位在教育和科研领域的应用将更加广泛和深入。因此，掌握力矩单位的概念、计算方法和应用场景对于物理学和工程学领域的学习者和从业者来说至关重要。