质因数分解的方法
质因数分解,作为数学中的一个基本概念,不仅在数学本身的研究中占据重要地位,还在密码学、计算机科学等多个领域有着广泛的应用。简单来说,质因数分解就是将一个正整数表示为若干个质数的乘积的过程。下面,我们将从基础概念出发,逐步深入探讨质因数分解的方法、步骤以及其在现实中的应用。
一、质数与合数的概念
在正式讨论质因数分解之前,我们需要明确两个基础概念:质数和合数。

质数:一个大于1的自然数,除了1和它本身以外不再有其他因数。例如,2、3、5、7等都是质数。
合数:一个大于1的自然数,除了1和它本身以外还有其他因数。例如,4、6、8、9等都是合数。
需要注意的是,1既不是质数也不是合数,而所有的质数都是奇数(除了2以外),但并非所有的奇数都是质数。
二、质因数分解的定义与意义
质因数分解,就是将一个合数表示为若干个质数的乘积。这个过程在数学上具有深远的意义。首先,它提供了一种将复杂数分解为更简单单元的方法;其次,质因数分解是理解数论中许多现象的基础,如费马小定理、欧拉定理等;最后,质因数分解在解决实际问题,如密码破解、数据加密等方面发挥着关键作用。
三、质因数分解的方法
质因数分解的方法主要分为试除法、分解质因数定理和筛选法三种。
1. 试除法
试除法是最直观、最基本的质因数分解方法。具体步骤如下:
从最小的质数2开始,用该质数去除待分解的数。
如果能整除,则记下这个质数,并将商作为新的待分解数继续尝试。
如果不能整除,则换下一个质数继续尝试,直到待分解数变为1为止。
所有记下的质数即为该数的质因数。
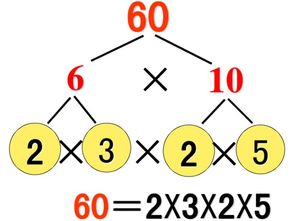
例如,对数字30进行质因数分解:
30 ÷ 2 = 15,记下2。
15 ÷ 3 = 5,记下3。
5是质数,无需再分解。
因此,30的质因数分解为2 × 3 × 5。
2. 分解质因数定理
分解质因数定理表明,任何一个大于1的自然数都可以唯一地分解为若干个质数的乘积。这个定理保证了质因数分解的唯一性,使得质因数分解成为了一个有意义且确定的过程。
3. 筛选法
筛选法主要用于寻找一定范围内的所有质数,而非直接对某个特定数进行质因数分解。但了解筛选法有助于我们更好地理解质数的分布规律,进而在质因数分解时做出更合理的选择。常见的筛选法有埃拉托斯特尼筛法和线性筛法等。
四、质因数分解的步骤与示例
下面,我们以一个具体的例子来演示质因数分解的步骤:
例:对数字100进行质因数分解。
步骤一:从最小的质数2开始尝试。
步骤二:100 ÷ 2 = 50,记下2,待分解数变为50。
步骤三:50 ÷ 2 = 25,再次记下2,待分解数变为25。
步骤四:25 ÷ 2 不整除,换下一个质数3尝试,也不整除。继续换下一个质数5尝试。
步骤五:25 ÷ 5 = 5,记下5,待分解数变为5。
步骤六:5是质数,无需再分解。
结果:因此,100的质因数分解为2² × 5²。
五、质因数分解的应用
质因数分解在多个领域有着广泛的应用。
1. 密码学
在密码学中,质因数分解是许多加密算法的基础。例如,RSA加密算法就依赖于大质数的分解难度。如果攻击者能够高效地分解一个大的合数为其质因数,那么RSA加密就会失去安全性。因此,寻找大质数和保护大质数不被分解成为了密码学研究的重要课题。
2. 计算机科学
在计算机科学中,质因数分解被用于优化算法和数据结构。例如,在素性测试(判断一个数是否为质数)中,质因数分解是一个重要的步骤。此外,质因数分解还有助于设计更高效的哈希函数和伪随机数生成器等。
3. 数学研究
在数学研究中,质因数分解是理解数论、代数和几何等领域中许多现象的基础。例如,费马小定理和欧拉定理等数论中的基本定理都依赖于质因数分解。此外,质因数分解还有助于解决一些组合数学问题,如整数划分等。
六、结论
质因数分解作为数学中的一个基本概念,不仅具有理论上的重要性,还在实际应用中发挥着关键作用。通过试除法、分解质因数定理和筛选法等方法,我们可以对一个合数进行质因数分解,进而更好地理解其结构和性质。同时,质因数分解在密码学、计算机科学和数学研究等多个领域的应用也展示了其广泛的实用价值。因此,掌握质因数分解的方法和应用对于深入学习数学和解决实际问题具有重要意义。
- 上一篇: 联通客服人工服务热线,一键直拨咨询台
- 下一篇: 深情的同义词探究
-
 揭秘:蛋白质分解酵素的神奇功效与作用!资讯攻略01-20
揭秘:蛋白质分解酵素的神奇功效与作用!资讯攻略01-20 -
 生长因子注射后,如何安全有效地进行取出?资讯攻略03-10
生长因子注射后,如何安全有效地进行取出?资讯攻略03-10 -
 探索“石”字的正确笔顺与笔画书写奥秘资讯攻略02-05
探索“石”字的正确笔顺与笔画书写奥秘资讯攻略02-05 -
 揭秘:最有效的十大解酒饮料,让你轻松应对酒后不适!资讯攻略01-13
揭秘:最有效的十大解酒饮料,让你轻松应对酒后不适!资讯攻略01-13 -
 掌握'恐怕'的正确发音:恐怕怎么读?资讯攻略04-10
掌握'恐怕'的正确发音:恐怕怎么读?资讯攻略04-10 -
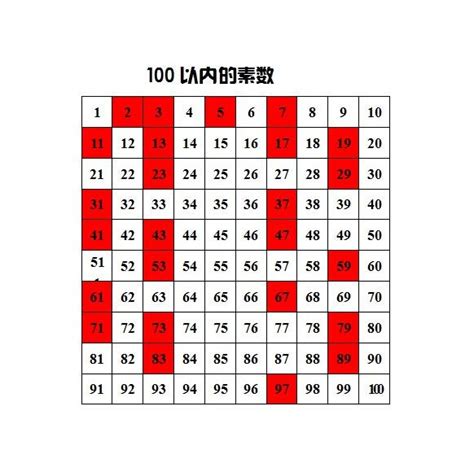 揭秘质数列:数学中的神秘贵族资讯攻略03-10
揭秘质数列:数学中的神秘贵族资讯攻略03-10












