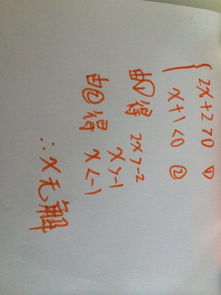数学中IAI的含义是什么

数学中的IAI是什么意思

在数学的广阔天地里，各种符号和表达式构成了其独特的语言。在这些符号中，“IAI”这一组合虽然并不常见作为一个整体的数学术语，但若将其拆解并理解为“|a|”（即a的绝对值），则能揭示出它在数学中的重要地位和意义。本文将深入探讨数学中绝对值的概念、性质、几何与代数意义，以及其在不同数学领域中的应用，旨在为读者提供一个全面而深入的理解。

一、绝对值的概念

绝对值，用数学符号“|a|”表示，读作“a的绝对值”，它表示一个数a距离数轴原点的距离。这个距离总是非负的，因此绝对值的值域是非负实数集。具体来说：

当a是非负数（包括正数和0）时，|a|的值就是a本身。

当a是负数时，|a|的值是a的相反数，即-a。

二、绝对值的性质

绝对值作为数学中的一个基本概念，具有一系列重要的性质，这些性质在数学推理和计算中发挥着关键作用。

1. 非负性：对于任意实数a，|a|≥0。这是绝对值定义的直接结果，也是其最基本的性质。

2. 绝对值不等式：对于任意实数a和b，若|a|≤|b|，则-b≤a≤b。这一性质揭示了绝对值与数轴上点之间距离的关系。

3. 绝对值的三角不等式：对于任意实数a和b，有|a+b|≤|a|+|b|。这一不等式在证明和估计中非常有用。

4. 绝对值的平方：对于任意实数a，有|a|^2=a^2。这一性质将绝对值与平方运算联系起来，为数学中的许多证明提供了便利。

5. 绝对值的可乘性：对于任意非负实数a和b，有|ab|=|a|×|b|。这一性质在代数运算中具有重要意义。

三、绝对值的几何意义

在几何上，绝对值可以理解为数轴上一点到原点的距离。这一解释不仅直观易懂，而且为绝对值的代数性质提供了几何直观。例如，绝对值的非负性可以看作是距离总是正的或零；绝对值的三角不等式可以看作是三角形两边之和大于第三边在数轴上的体现。

四、绝对值的代数意义

在代数上，绝对值具有更丰富的意义。它不仅表示一个数到原点的距离，还反映了该数的正负性质。具体来说：

正数的绝对值是它本身，这反映了正数在数轴上位于原点的右侧，其距离就是它本身。

负数的绝对值是它的相反数，这反映了负数在数轴上位于原点的左侧，其距离需要取相反数以表示为正数。

零的绝对值是零，这反映了零在数轴上就是原点本身，其距离为零。

五、绝对值在数学中的应用

绝对值在数学中有着广泛的应用，它不仅出现在基础代数和几何中，还贯穿于高等数学和实际应用领域。

1. 基础代数：在解不等式时，绝对值的概念经常被用到。例如，解不等式|x-3|≤5时，需要分别考虑x-3为正、负和零三种情况。此外，在代数式的化简和求值中，绝对值也发挥着重要作用。

2. 几何：在几何学中，绝对值可以用来表示点到点的距离、点到直线的距离等。这些距离概念是几何学的基础，也是解决几何问题的重要工具。

3. 高等数学：在高等数学中，绝对值的概念被推广到复数域、向量空间等更广泛的数学结构中。此外，在极限、导数、积分等微积分概念中，绝对值也经常出现。

4. 实际应用：绝对值在物理学、工程学、经济学等领域有着广泛的应用。例如，在物理学中，绝对值可以用来表示力、速度、加速度等物理量的大小；在经济学中，绝对值可以用来表示利润、亏损等经济指标的大小。

六、绝对值与数学其他概念的联系

绝对值作为数学中的一个基本概念，与其他数学概念之间存在着密切的联系。例如：

绝对值与范数：在向量空间和赋范空间中，绝对值的概念被推广到范数的概念。范数是向量空间中元素大小的度量，它满足非负性、齐次性和三角不等式等性质，这些性质与绝对值的性质相似。

绝对值与模运算：在整数运算中，模运算是一种重要的运算方式。模运算的结果是两个整数相除的余数，这个余数可以用绝对值来表示。此外，在数论中，绝对值还与同余、整除等概念密切相关。

绝对值与不等式：绝对值在不等式中经常出现，它使得不等式问题变得更加复杂和多样化。解决这类问题通常需要运用绝对值的性质和运算规则进行化简和转化。

七、结论

综上所述，数学中的“IAI”（即绝对值）是一个具有深刻内涵和广泛应用的概念。它不仅是数学基础的重要组成部分，也是解决实际问题的重要工具。通过深入理解绝对值的定义、性质、几何与代数意义以及其在不同数学领域中的应用，我们可以更好地掌握数学这门学科的知识和方法，为解决实际问题提供有力的数学支持。同时，我们也应该注意到绝对值与其他数学概念之间的联系和区别，以便在数学学习和研究中形成更加完整和系统的知识体系。