探索平均方差的求解奥秘
平均方差求解指南

在统计学中,平均方差是衡量数据离散程度的一个重要指标,它描述了数据与其平均值之间的偏差程度。平均方差(Variance)的计算在数据分析、金融风险评估、质量控制等多个领域都有广泛应用。下面,我们将详细介绍如何计算平均方差。

一、基本概念
1. 均值(Mean):
均值是所有数据值的总和除以数据的个数,它反映了数据的“平均水平”。
数学公式表示为:
\[ \text{Mean} = \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]
其中,\( n \) 是数据个数,\( x_i \) 是每一个数据值。
2. 方差(Variance):
方差是每个数据值与均值之差的平方的平均值,它衡量了数据分布的离散程度。
数学公式表示为:
\[ \text{Variance} = s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]
其中,\( s^2 \) 表示方差,\( (x_i - \bar{x})^2 \) 是每个数据值与均值之差的平方。
二、计算步骤
为了更清晰地说明如何计算平均方差,我们通过一个具体的例子来演示。
假设我们有一组数据:\( 5, 7, 8, 9, 10 \)
1. 计算均值:
首先,我们需要计算这组数据的均值。
\[ \bar{x} = \frac{5 + 7 + 8 + 9 + 10}{5} = \frac{39}{5} = 7.8 \]
2. 计算每个数据值与均值之差的平方:
接下来,我们计算每个数据值与均值之差的平方。
\[ (5 - 7.8)^2 = (-2.8)^2 = 7.84 \]
\[ (7 - 7.8)^2 = (-0.8)^2 = 0.64 \]
\[ (8 - 7.8)^2 = 0.2^2 = 0.04 \]
\[ (9 - 7.8)^2 = 1.2^2 = 1.44 \]
\[ (10 - 7.8)^2 = 2.2^2 = 4.84 \]
3. 计算方差:
最后,我们将这些平方差相加,然后除以数据的个数,得到方差。
\[ s^2 = \frac{7.84 + 0.64 + 0.04 + 1.44 + 4.84}{5} = \frac{14.8}{5} = 2.96 \]
所以,这组数据的方差为 2.96。
三、方差的应用
1. 衡量数据离散程度:
方差越大,说明数据分布越离散,即数据之间的差异越大;方差越小,说明数据分布越集中,即数据之间的差异越小。
2. 风险评估:
在金融领域,方差常用于评估投资组合的风险。一个投资组合的方差越大,说明其收益波动越大,风险也越高。
3. 质量控制:
在生产过程中,方差可用于监控产品的质量稳定性。如果产品的方差较大,说明产品质量不稳定,需要采取措施进行改进。
四、注意事项
1. 样本方差与总体方差:
在计算方差时,需要注意是计算样本方差还是总体方差。样本方差通常使用 \( n-1 \) 作为分母(称为贝塞尔校正),以更好地估计总体方差;而总体方差则使用 \( n \) 作为分母。
样本方差公式:
\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]
总体方差公式:
\[ \sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2 \]
其中,\( \mu \) 表示总体均值。
2. 数据预处理:
在计算方差之前,通常需要对数据进行预处理,如去除异常值、标准化等,以确保计算结果的准确性和可靠性。
3. 方差的性质:
方差具有一些重要的性质,如方差不受数据整体平移的影响(即数据加减一个常数后,方差不变);但数据乘以一个常数 \( k \) 后,方差会变为 \( k^2 \) 倍。
五、总结
平均方差是衡量数据离散程度的重要指标,通过计算每个数据值与均值之差的平方的平均值,我们可以得到数据的方差。方差在数据分析、金融风险评估、质量控制等多个领域都有广泛应用。在计算方差时,需要注意区分样本方差和总体方差,并进行适当的数据预处理。通过掌握方差的计算方法和应用,我们可以更好地理解和分析数据,为决策提供有力支持。
- 上一篇: 揭秘!12月25日:历史上的今天发生了哪些大事?
- 下一篇: 揭秘:利好与利空,股市波动的神秘密码
-
 求解:五体投地姿态代表的生肖是什么?资讯攻略03-09
求解:五体投地姿态代表的生肖是什么?资讯攻略03-09 -
 如何求解集合A={1,3,5,6}与集合B={2,3,4,5}的并集AUB?资讯攻略02-02
如何求解集合A={1,3,5,6}与集合B={2,3,4,5}的并集AUB?资讯攻略02-02 -
 MATLAB中如何高效求解指数函数资讯攻略03-22
MATLAB中如何高效求解指数函数资讯攻略03-22 -
 求解仙剑3 GDB修改器使用问题资讯攻略04-23
求解仙剑3 GDB修改器使用问题资讯攻略04-23 -
 2022年全国一卷数学平均分揭晓!资讯攻略03-11
2022年全国一卷数学平均分揭晓!资讯攻略03-11 -
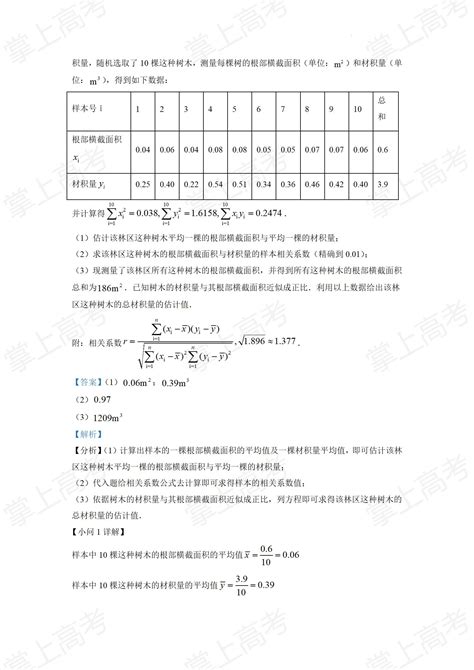 2022年全国乙卷数学平均分大揭秘!资讯攻略01-27
2022年全国乙卷数学平均分大揭秘!资讯攻略01-27












