ln2的值是多少？

在数学的浩瀚宇宙中，有一个看似简单却蕴藏着无穷奥秘的数字——自然对数的底数ln2。它不仅是数学中的一个基本常数，更是连接着数学、物理学、计算机科学乃至生物学等多个领域的桥梁。本文将从数学定义、计算历史、实际应用以及文化寓意等多个维度，探索ln2这一神奇数字背后的故事。

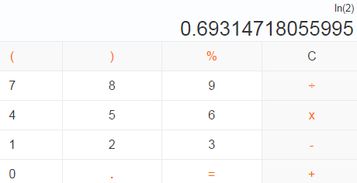
数学定义：ln2，自然对数的奥秘

在数学上，自然对数是以数学常数e（约等于2.71828）为底的对数。而ln2，即为以e为底2的对数值。这个定义初看之下可能略显抽象，但实际上，它反映了2作为自然增长模型中的一个基本单位，在连续复利增长或放射性衰变等自然现象中的变化规律。ln2的值约为0.69314718056，这个数值虽然无法表示为有限小数或分数，但它在数学分析、微积分等领域中扮演着至关重要的角色。

计算历史：从古至今的探索之旅

人类对ln2的探索可以追溯到对数概念的诞生。17世纪，苏格兰数学家约翰·纳皮尔斯在解决天文计算中的复杂乘法问题时，首次提出了对数的概念。随后，瑞士数学家欧拉在深入研究对数函数的基础上，引入了自然对数，并将e作为自然对数的底数。尽管当时没有现代计算工具，但数学家们已经开始尝试通过各种方法逼近ln2的值。

随着计算技术的发展，特别是电子计算机的出现，ln2的精确值逐渐被确定到更多的小数位。如今，借助高精度的数值计算方法，我们可以轻松获得ln2的近似值，甚至在某些专业软件中，可以查询到其超过亿位小数的精确值。这一计算历程，不仅见证了人类对数学常数追求精确的精神，也反映了科技进步对数学研究的重要推动作用。

实际应用：从物理学到计算机科学

ln2的应用广泛而深刻，几乎渗透到了科学的每一个角落。在物理学中，ln2与放射性衰变、热力学过程等自然现象紧密相连。例如，在放射性同位素衰变的研究中，ln2可以帮助科学家预测衰变产物的比例随时间的变化。在热力学中，ln2与熵增原理有关，揭示了系统在自发过程中倾向于增加混乱度的规律。

在计算机科学领域，ln2更是信息论中的核心概念之一。信息论由克劳德·香农创立，旨在量化信息的传输和存储效率。在香农的信息理论中，信息熵是衡量信息不确定性的度量，而ln2作为自然对数的底数，在计算信息熵时起着关键作用。此外，在算法分析、数据压缩等领域，ln2也是评估算法效率和数据冗余度的重要工具。

生物学启示：遗传密码中的微妙平衡

ln2在生物学领域同样有着令人惊讶的应用。在遗传学研究中，ln2与基因突变率、物种多样性等生物进化过程中的关键参数息息相关。例如，在分子进化生物学中，通过比较不同物种间基因序列的差异，科学家可以利用ln2来估算基因突变的速率，进而推断物种的分歧时间和进化历程。此外，ln2还与物种多样性的维持机制有关，揭示了自然界中物种数量与生态位占用之间的微妙平衡。

文化寓意：数学之美与人生哲理

除了在科学领域的应用外，ln2还蕴含着丰富的文化寓意和人生哲理。从数学美学的角度来看，ln2作为自然对数的一个基本常数，其简洁而深邃的表达式体现了数学之美。它像一座桥梁，连接着看似无关的数学概念，展现了数学内在的统一性和和谐性。

在人生哲理方面，ln2的连续增长特性启示我们，无论是个人成长还是社会发展，都需要经历一个不断积累、逐渐突破的过程。正如ln2所反映的，即使在看似平缓的增长曲线中，也蕴含着无限的可能性和潜力。因此，面对生活中的挑战和困难，我们应该保持耐心和坚持，相信每一次微小的进步都是通往成功之路上的宝贵积累。

结语：ln2，连接科学与人文的桥梁

综上所述，ln2作为自然对数的底数，不仅在数学领域具有重要地位，更在物理学、计算机科学、生物学乃至文化寓意等多个维度上展现出了其独特的魅力和价值。它像一座桥梁，连接着科学与人文，启示着我们探索未知、追求真理的精神。在未来的科学研究中，随着我们对ln2的深入理解和应用，相信它将继续引领我们走向更加广阔的知识天地，揭示更多自然界的奥秘和人生的哲理。