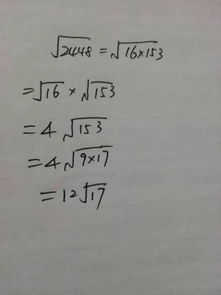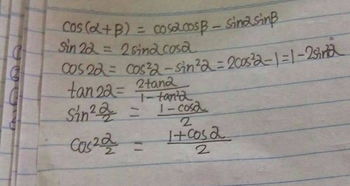sin15°的计算结果是多少?
在数学中,角度与三角函数的关系是基础而重要的知识点。其中,sin函数,即正弦函数,表示一个锐角对应的直角三角形的对边与斜边的比值。当我们需要求解sin15度(sin15°)的具体值时,这个问题看似简单,实则涉及到了三角函数的基本性质和一定的计算技巧。

首先,我们回顾一下三角函数的定义。对于一个锐角θ,其对应的直角三角形中,sinθ等于对边长度除以斜边长度。然而,当θ不是特殊角(如30°、45°、60°)时,直接通过定义求解sinθ的值就变得较为复杂。这是因为对于非特殊角,我们通常无法直接得到一个整数或简单的分数作为sinθ的值,而需要借助其他数学工具或方法进行求解。

对于sin15°的求解,我们可以采用多种方法。其中一种常见且有效的方法是利用两角和的正弦公式。这个公式是:sin(α+β)=sinαcosβ+cosαsinβ。我们可以将15°拆分为两个特殊角的和,比如45°和-30°,然后代入公式进行计算。
具体步骤如下:
第一步,确定α和β的值。在这里,我们设α=45°,β=-30°。注意,虽然-30°不是一个锐角,但在三角函数中,角度是可以扩展到全实数范围的,只是在实际应用中,我们通常只关注0°到360°(或0到2π)的范围。不过,在这个问题中,使用-30°可以简化计算过程。
第二步,代入两角和的正弦公式。我们得到:sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°。
第三步,计算各个特殊角的三角函数值。我们知道,sin45°=√2/2,cos30°=√3/2,cos45°=√2/2,sin30°=1/2。
第四步,将上述值代入公式进行计算。我们得到:sin15°=(√2/2)×(√3/2)-(√2/2)×(1/2)=(√6-√2)/4。
这个结果是经过精确计算得出的,它表示了sin15°的确切值。在实际应用中,我们可以根据需要保留一定的小数位数来近似表示这个值。
除了使用两角和的正弦公式外,我们还可以利用其他方法来求解sin15°的值。比如,我们可以利用三角函数的半角公式。这个公式是:sin(θ/2)=±√[(1-cosθ)/2]。在这个问题中,我们可以将θ设为30°,然后利用半角公式求出sin15°的值。但是需要注意的是,由于sin函数在0°到180°之间是单调递增的,因此当θ=30°时,sin(θ/2)应该取正值。
具体步骤如下:
第一步,确定θ的值。在这里,我们设θ=30°。
第二步,代入半角公式。我们得到:sin15°=sin(30°/2)=√[(1-cos30°)/2]。
第三步,计算cos30°的值。我们知道,cos30°=√3/2。
第四步,将上述值代入公式进行计算。我们得到:sin15°=√[(1-(√3/2))/2]=√[(2-√3)/4]=(√6-√2)/4。这个结果与使用两角和的正弦公式得到的结果是一致的。
另外,我们还可以利用三角函数的和差化积公式或倍角公式来求解sin15°的值。这些公式都是三角函数的基本性质之一,它们在不同的应用场景下具有各自的优点和适用范围。在求解sin15°的值时,我们可以根据具体情况选择最合适的方法进行计算。
值得注意的是,虽然上述方法都可以求出sin15°的确切值,但在实际应用中,我们有时并不需要这么精确的结果。比如,在工程设计或物理实验中,我们可能只需要知道sin15°的近似值就足够了。在这种情况下,我们可以使用计算器或查阅三角函数表来快速获取sin15°的近似值。这些工具通常会给出一定精度范围内的近似结果,足以满足大多数实际应用的需求。
此外,在学习三角函数的过程中,我们还需要注意一些常见的误区和易错点。比如,有些同学可能会混淆正弦、余弦和正切函数的定义和性质;有些同学可能会在计算过程中忽略角度的单位或正负号;还有些同学可能会误用三角函数的公式或定理等。为了避免这些错误,我们需要认真学习和理解三角函数的基本概念、性质和公式等知识点,并多做练习来巩固和提高自己的计算能力。
总之,求解sin15°的值是一个涉及三角函数基本性质和计算技巧的问题。通过采用不同的方法和工具进行计算和验证,我们可以得到sin15°的确切值或近似值,并根据具体需求选择合适的表示方式。在学习三角函数的过程中,我们需要注重理解和掌握基本概念、性质和公式等知识点,并注意避免常见的误区和易错点。同时,我们还需要多做练习和实践来巩固和提高自己的计算能力,以便更好地应用三角函数解决实际问题。
-
 90除以5的结果是多少?请提供竖式计算资讯攻略01-12
90除以5的结果是多少?请提供竖式计算资讯攻略01-12 -
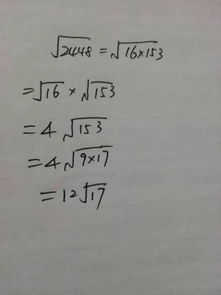 548的算术平方根计算结果是多少?资讯攻略04-06
548的算术平方根计算结果是多少?资讯攻略04-06 -
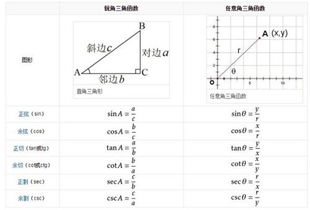 sec(x)的倒数是sin(x)还是cos(x)?资讯攻略04-05
sec(x)的倒数是sin(x)还是cos(x)?资讯攻略04-05 -
 计算机丢失ijl15.dll的解决方法资讯攻略01-22
计算机丢失ijl15.dll的解决方法资讯攻略01-22 -
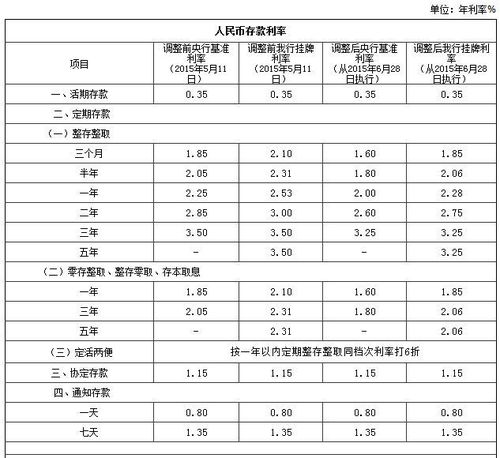 5万邮政储蓄三年定期存款利息是多少?资讯攻略01-12
5万邮政储蓄三年定期存款利息是多少?资讯攻略01-12 -
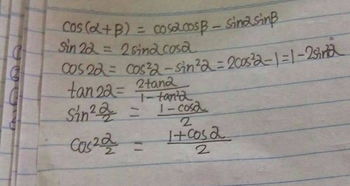 sin(α)cos(α)的公式是什么?资讯攻略02-02
sin(α)cos(α)的公式是什么?资讯攻略02-02