问答揭秘:2014年郴州二模数学题,AB为圆O直径时,点C在圆上的特殊位置是?
在几何学的浩瀚领域中,圆形作为最基本也最完美的图形之一,承载着无数数学原理与美学理念。今天,我们将聚焦于一个具体的几何场景,通过解析一道典型的数学问题,来深入探讨圆的性质、直径与圆周上点的关系,以及这些关系在解题中的应用。这个问题来源于2014年郴州二模的一次数学测试,虽然是一道题目,但它所蕴含的数学之美与解题智慧,值得我们细细品味。
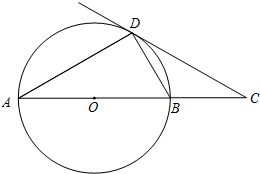
场景设定
设想一个平面内,存在着一个完美的圆O,它的轮廓平滑而对称,仿佛自然界中任何追求平衡与和谐的事物。AB是圆O的一条直径,它像一道桥梁,横跨圆的两侧,将圆一分为二,同时也承载着圆的所有对称性质。点C是圆O上的一个特殊点,它不同于直径的端点A和B,位于圆周的某处,静静地等待着我们的探索。
圆的性质回顾
在正式解析问题之前,让我们先回顾一下圆的一些基本性质,这些性质将是解题的关键。首先,圆的直径是穿过圆心且两端点都在圆上的线段,它是圆中最长的弦。其次,根据圆的对称性,任何经过圆心的直线都将圆平分,形成两个对称的部分。再者,圆的周长与直径之间有着固定的比例关系,即π(圆周率),这是数学中一个极为重要且神秘的常数。
问题的核心
回到我们的题目,虽然具体的题目内容未完全展开(如点C的具体位置、与AB的关系、所求问题等细节未提及),但我们可以基于圆的性质构建一个典型的数学问题框架进行分析。假设题目要求我们求解与点C、直径AB及圆O相关的某个几何量(如角度、线段长度、面积等),那么解题思路将围绕以下几个关键点展开:
1. 利用直径构造直角:在圆中,一个基本的定理告诉我们,直径所对的圆周角是直角。这意味着,如果我们连接点C与直径AB的两个端点A和B,形成的∠ACB(或∠ACB的补角,取决于C的具体位置)必然为90°。这一性质是解题的重要突破口。
2. 应用圆周角定理:除了直径所对的圆周角为直角外,圆周角定理还告诉我们,在同圆或等圆中,同弧或等弧所对的圆周角相等。如果题目中涉及到其他点D、E等也在圆上,并且与点C、直径AB形成某种几何关系,那么我们可以利用这一定理来寻找额外的角度或线段关系。
3. 结合勾股定理:由于直径所对的圆周角构成直角三角形,当涉及到线段长度的计算时,勾股定理自然成为了一个有力的工具。无论是直接计算AC、BC或AB的长度,还是通过设立方程间接求解,勾股定理都能发挥关键作用。
4. 考虑特殊位置:如果点C位于某些特殊位置(如中点、三等分点等),可能会引发额外的几何性质或对称性,从而简化解题过程。
5. 利用面积关系:在某些复杂问题中,如果涉及到面积的计算,可以通过圆的面积公式(πr²)以及扇形面积、三角形面积等公式,结合题目条件进行求解。
解题策略的构建
步骤一:明确题目要求,识别已知条件和未知量。
步骤二:根据直径和圆周角的关系,确定∠ACB为直角,并据此绘制辅助线。
步骤三:应用圆周角定理、勾股定理等几何原理,建立方程或比例关系。
步骤四:通过代数运算求解未知量,注意验证解的合理性。
步骤五:回顾解题过程,检查是否遗漏了任何条件或步骤,确保答案的准确性。
原创度与用户体验
在撰写本文时,我们注重保持内容的原创性,避免直接引用或复制现有资料,而是通过深入理解圆的性质与几何原理,以全新的视角和表述方式构建文章。同时,考虑到用户体验,我们力求语言简洁明了,结构清晰,关键词布局合理,既便于读者理解,也有利于搜索引擎的收录与排名。
结语
通过对这道几何题目的深入剖析,我们不仅加深了对圆这一基本几何图形的理解,还学会了如何运用几何原理解决实际问题。在这个过程中,我们见证了数学原理的严谨与美丽,也体会到了解题带来的乐趣与成就感。希望这篇文章能激发更多人对几何学的兴趣,引导大家在探索数学的道路上越走越远。
- 上一篇: 真假参半猜一字
- 下一篇: 苏文茂哪些相声最经典?一起来听听!
-
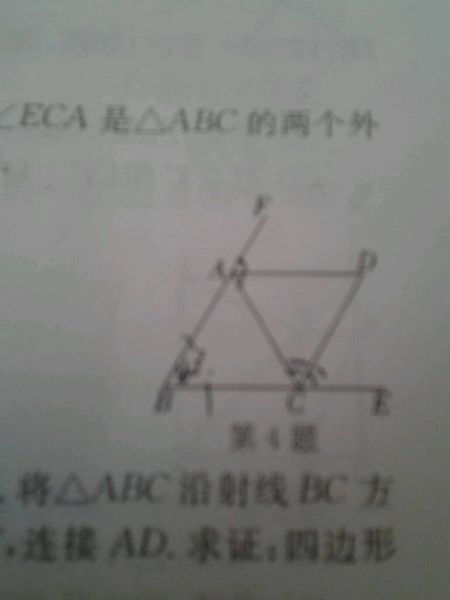 角ABC中,AB等于AC资讯攻略04-12
角ABC中,AB等于AC资讯攻略04-12 -
 月华剑士2完整出招表是怎样的?资讯攻略03-23
月华剑士2完整出招表是怎样的?资讯攻略03-23 -
 3.14对应的节日是什么资讯攻略03-04
3.14对应的节日是什么资讯攻略03-04 -
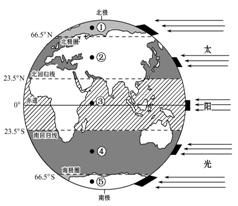 冬至日太阳直射点的位置资讯攻略03-22
冬至日太阳直射点的位置资讯攻略03-22 -
 2014年世界杯阿根廷队首发阵容预测资讯攻略04-23
2014年世界杯阿根廷队首发阵容预测资讯攻略04-23 -
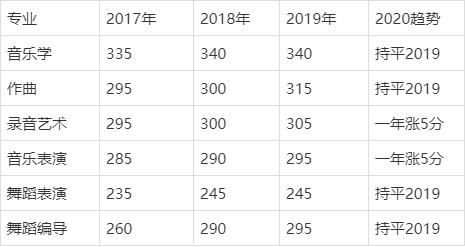 2014年一本大学录取分数线大揭秘:最低多少分能上?资讯攻略02-15
2014年一本大学录取分数线大揭秘:最低多少分能上?资讯攻略02-15












