角ABC中,AB等于AC
探索等腰三角形的奥秘:在角ABC中,AB=AC的奇妙世界
在几何学的浩瀚宇宙中,三角形以其简洁而稳定的结构,成为了无数数学家和爱好者们探索的乐园。而在三角形的众多形态中,等腰三角形以其独特的对称美和内在性质,尤为引人注目。今天,就让我们一同踏入等腰三角形的神秘殿堂,特别是在角ABC中,当AB=AC时,那隐藏于简单条件之下的无尽奥秘。

一、等腰三角形的定义与直观感受
等腰三角形,顾名思义,就是两边长度相等的三角形。在角ABC中,若AB=AC,则三角形ABC即为等腰三角形。直观上看,等腰三角形具有一种难以言喻的和谐美。它的两边对称地分布在底边两侧,仿佛是大自然赋予的一种平衡与秩序。而这种直观上的美感,正是吸引我们去深入探究其内在性质的原动力。

二、等腰三角形的性质探索
2.1 底边上的中线、高线和顶角的平分线重合
在等腰三角形ABC中,AB=AC,我们可以发现一条重要的性质:底边BC上的中线AD(D为BC的中点)、高线AD(AD垂直于BC)以及顶角∠BAC的平分线AD是重合的。这一性质被称为等腰三角形的“三线合一”。它揭示了等腰三角形内在的一种简洁与统一,也为我们在解决实际问题时提供了极大的便利。
想象一下,当我们面对一个复杂的等腰三角形问题时,只需要找到底边上的中线、高线或顶角的平分线中的任意一条,就可以同时掌握其他两条线的信息。这种“一线在手,三线我有”的奇妙感受,无疑增添了等腰三角形的魅力。
2.2 底角相等
在等腰三角形ABC中,由于AB=AC,根据等腰三角形的性质,我们可以得出底角∠B=∠C。这一性质看似简单,却蕴含着深刻的几何意义。它告诉我们,在等腰三角形中,底边的两个端点与顶角之间的夹角是相等的。这种对称性不仅体现在边的长度上,更体现在角的大小上。
底角相等的性质在实际应用中同样具有广泛的价值。比如,在建筑设计、工程测量等领域,我们经常需要确保某些结构的对称性。此时,等腰三角形的底角相等性质就可以为我们提供一个精确的度量标准。
2.3 顶角的平分线与底边平行且等于底边的一半
在等腰三角形ABC中,若我们延长顶角∠BAC的平分线AD至点E,使得DE平行于BC,则根据等腰三角形的性质,我们可以得出DE=BC/2。这一性质虽然不如“三线合一”和底角相等那样直观,但它在某些特定的问题中却发挥着举足轻重的作用。
比如,在求解某些与等腰三角形相关的线段长度问题时,我们可以巧妙地利用这一性质,将复杂的几何问题转化为简单的代数问题,从而大大简化解题过程。
三、等腰三角形的应用实例
等腰三角形在日常生活和科学研究中的应用无处不在。下面,我们就来探讨几个具体的实例。
3.1 建筑设计与装饰艺术
在建筑设计和装饰艺术中,等腰三角形经常被用作构建对称和平衡感的元素。比如,在古罗马建筑中,拱门和穹顶就经常采用等腰三角形的结构,以展现其宏伟与庄严。而在现代装饰艺术中,等腰三角形也常被用作图案设计的基础元素,以营造出一种简洁而富有层次感的视觉效果。
3.2 工程测量与定位
在工程测量和定位领域,等腰三角形的性质同样发挥着重要作用。比如,在测量某段直线的长度时,我们可以利用等腰三角形的底边等于两腰之和的性质,通过测量两腰的长度来间接求得底边的长度。这种方法不仅简单易行,而且具有较高的精度。此外,在等腰三角形的顶点处设置定位装置,还可以实现对目标区域的精确定位和跟踪。
3.3 物理与力学分析
在物理和力学领域,等腰三角形的性质也被广泛应用于各种分析和计算中。比如,在分析梁的弯曲变形时,我们可以将梁看作是由无数个等腰三角形组成的连续体,从而利用等腰三角形的性质来求解梁的弯曲应力和变形量。这种方法不仅提高了计算的准确性,而且为梁的优化设计和加固提供了有力的理论依据。
四、等腰三角形的美学价值与文化内涵
等腰三角形不仅在科学研究中具有广泛的应用价值,在美学领域也占据着举足轻重的地位。它的对称美和内在性质不仅激发了艺术家们的创作灵感,也成为了连接科学与艺术的桥梁。
在许多古代文明中,等腰三角形都被视为一种神圣的象征。比如,在埃及金字塔的设计中,等腰三角形的结构就被巧妙地运用到了建筑的稳定性和美观性的结合上。而在现代艺术中,等腰三角形也经常被用作表达简约、和谐与平衡感的元素。
此外,等腰三角形还与数学、物理、化学等多个学科领域紧密相连。它的性质被广泛应用于各种科学理论和实际问题中,成为连接不同学科领域的纽带。这种跨学科的价值不仅丰富了等腰三角形的内涵,也为我们提供了更广阔的视野和更深入的理解。
五、结语
在角ABC中,当AB=AC时,我们踏入了一个充满奥秘与美丽的等腰三角形世界。从直观的对称美到深刻的内在性质,从广泛的应用实例到丰富的美学价值与文化内涵,等腰三角形以其独特的魅力吸引着我们不断探索和发现。
在这个旅程中,我们不仅领略了等腰三角形的几何之美,更深刻体会到了科学探索的乐趣和意义。让我们带着这份对美的追求和对知识的渴望,继续前行在几何学的广阔天地中,去发现更多未知的美妙与奇迹吧!
- 上一篇: 揭秘:二十国集团究竟囊括了哪些全球经济巨擘?
- 下一篇: 魔兽世界:如何快速前往暮光高地?传送门指南!
-
 街舞AC是何许人也?资讯攻略03-09
街舞AC是何许人也?资讯攻略03-09 -
 AC-130U特种作战飞机核心性能概述资讯攻略04-14
AC-130U特种作战飞机核心性能概述资讯攻略04-14 -
 sin15°的计算结果是多少?资讯攻略02-07
sin15°的计算结果是多少?资讯攻略02-07 -
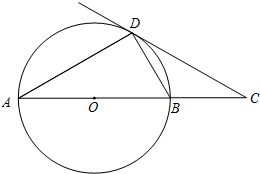 问答揭秘:2014年郴州二模数学题,AB为圆O直径时,点C在圆上的特殊位置是?资讯攻略03-21
问答揭秘:2014年郴州二模数学题,AB为圆O直径时,点C在圆上的特殊位置是?资讯攻略03-21 -
 魔角侦探主题曲歌词优化版资讯攻略03-08
魔角侦探主题曲歌词优化版资讯攻略03-08 -
 月华剑士2完整出招表是怎样的?资讯攻略03-23
月华剑士2完整出招表是怎样的?资讯攻略03-23












