揭秘:根号2的精确值究竟是多少?
根号2,这个数学中的经典常数,自古以来就吸引着无数数学家和学者的目光。它不仅仅是一个简单的无理数,更是连接有理数和无理数世界的桥梁,是数学史上许多重大发现的催化剂。那么,根号2究竟等于多少呢?
要解答这个问题,我们首先需要理解什么是根号。在数学中,根号(通常表示为√)是一个运算符,用于求一个数的平方根。如果一个数x的平方等于另一个数y,即x²=y,那么x就是y的平方根。特别地,正数y有两个平方根,一个正的和一个负的,因为(-x)²=x²。但当我们说“根号y”时,通常指的是非负的那个平方根,即算术平方根。

现在,让我们回到根号2这个问题上。根号2,即√2,表示2的算术平方根。换句话说,我们需要找到一个数,这个数的平方等于2。显然,这个数既不是整数也不是分数,而是一个无限不循环小数。因此,根号2是一个无理数。

历史上,根号2的发现与毕达哥拉斯定理(勾股定理)密切相关。毕达哥拉斯学派是古代希腊的一个数学学派,他们认为宇宙中的一切都可以用整数或分数的比例来表示。然而,这个信念在根号2的发现面前被彻底颠覆了。

相传,毕达哥拉斯的一个学生希帕索斯在研究正方形对角线与其边长之比时,发现了根号2的存在。他发现,如果一个正方形的边长为1,那么其对角线的长度就不能用整数或分数来表示,而是等于根号2。这个发现震惊了整个学派,因为它违背了毕达哥拉斯定理的原始假设——所有几何量都可以用有理数来表示。
希帕索斯的发现引发了学派内部的巨大争议。据说,毕达哥拉斯本人对此极为不满,甚至认为这是一种亵渎。为了维护学派的纯洁性,毕达哥拉斯下令将希帕索斯处死。这一事件在数学史上被称为“第一次数学危机”,它标志着人们开始认识到无理数的存在和重要性。
尽管根号2的发现充满了争议和悲剧,但它无疑为数学的发展开辟了新的道路。随着人们对无理数的逐渐接受和研究,数学理论得到了极大的丰富和完善。根号2作为无理数的代表之一,成为了数学家们探索未知世界的重要工具。
那么,根号2的具体值是多少呢?由于它是一个无限不循环小数,我们无法给出一个精确的有限小数表示。但我们可以使用各种方法来逼近它的值。例如,我们可以使用幂级数展开、连分数逼近或数值迭代等方法来计算根号2的近似值。
在实际应用中,我们通常只需要根号2的足够精确的近似值即可。例如,在计算机科学中,浮点数表示法允许我们以有限的精度来表示实数。对于根号2这样的无理数,我们可以使用足够多的有效数字来确保计算的准确性。
为了给出一个具体的近似值,我们可以使用计算器或编程语言来计算根号2的值。在现代计算机中,我们可以轻松得到根号2的高精度近似值。例如,使用Python编程语言中的math库函数sqrt()来计算根号2的值,我们可以得到以下结果:
```python
import math
sqrt_2 = math.sqrt(2)
print(sqrt_2)
```
运行这段代码后,我们将得到一个非常接近根号2真实值的浮点数表示。这个值可能因计算机精度和舍入误差而略有不同,但在大多数情况下,它足够精确以满足我们的需求。
除了计算器编程方法外,我们还可以使用手动计算的方法来逼近根号2的值。例如,我们可以使用牛顿迭代法或二分法等方法来逐步逼近根号2的真实值。这些方法虽然比较复杂和耗时,但它们为我们提供了一种不依赖计算机的手动计算方法。
最后,需要强调的是,尽管我们无法给出一个精确的有限小数表示来完全等于根号2,但我们可以通过各种方法来逼近它的值,并在实际应用中使用这些近似值进行计算和分析。根号2作为数学中的一个重要常数,不仅在理论上具有重要意义,而且在实际应用中也发挥着重要作用。
综上所述,根号2是一个无理数,它表示2的算术平方根。尽管我们无法给出一个精确的有限小数表示来完全等于它,但我们可以通过各种方法来逼近它的值,并在实际应用中使用这些近似值。根号2的发现不仅颠覆了毕达哥拉斯学派的原始假设,而且为数学的发展开辟了新的道路。作为无理数的代表之一,它将继续在数学和科学领域中发挥重要作用。
- 上一篇: 探寻1987年阴历11月23日对应的公历神秘日期
- 下一篇: 蚌埠装甲兵学院:揭秘其教育层次与实力!
-
 根号5的数值是多少资讯攻略04-28
根号5的数值是多少资讯攻略04-28 -
 揭秘!王者荣耀荣耀水晶幸运值满值究竟是多少?资讯攻略02-05
揭秘!王者荣耀荣耀水晶幸运值满值究竟是多少?资讯攻略02-05 -
 电脑如何打出根号?资讯攻略04-11
电脑如何打出根号?资讯攻略04-11 -
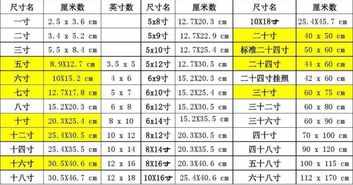 揭秘!2寸照片的标准尺寸究竟是多少?资讯攻略01-18
揭秘!2寸照片的标准尺寸究竟是多少?资讯攻略01-18 -
 揭秘!一升究竟是多少毫升?资讯攻略01-28
揭秘!一升究竟是多少毫升?资讯攻略01-28 -
 中秋最圆月,10月2日凌晨何时惊鸿一瞥?精确到秒!资讯攻略02-04
中秋最圆月,10月2日凌晨何时惊鸿一瞥?精确到秒!资讯攻略02-04












