根号5的数值是多少
根号五是多少

根号五,这个看似简单的数学表达式,实则蕴含了丰富的数学内涵和广泛的应用领域。它表示的是5的平方根,即一个数的平方等于5。换句话说,如果存在一个数a,使得a的平方等于5,那么a就是根号五的值。在实数范围内,根号五是一个无理数,它无法被精确地表示为一个分数,其值大约是2.236(通常精确到小数点后三位,但实际上是一个无限不循环小数)。

根号五的数学定义与性质
在数学上,平方根的定义是:对于任何正数b,存在两个数a和-a,它们的平方都等于b。这是因为负数的平方也是正数,所以平方根有两个可能的值,一个正数和一个负数。然而,在通常的数学语境中,当我们谈论一个数的平方根时,默认是指其正的平方根,即算术平方根。因此,根号五通常指的是正的平方根,即约等于2.236的那个数。

根号五作为无理数,具有无理数的所有基本性质。无理数是不能表示为两个整数的比的数,它们在数轴上表现为无限不循环的小数。无理数的这一特性使得它们在数学上非常独特,也增加了研究它们的难度和趣味性。

根号五的计算方法
根号五的值可以通过多种数学方法得到。其中,一些数值方法如牛顿迭代法和二分法特别适用于计算无理数的近似值。
牛顿迭代法:这是一种高效求解方程根的数值方法。对于根号五,我们可以构造一个方程f(x) = x² - 5,然后应用牛顿迭代法来求解这个方程的根。牛顿迭代法的迭代公式为:x_{n+1} = 0.5 * (x_n + 5 / x_n)。如果取初始猜测值x_0 = 2,经过几次迭代后,就可以得到根号五的近似值。
二分法:二分法是一种基于区间收缩的数值方法。对于根号五,我们可以在一个包含根号五值的区间内(例如[2, 3]),通过不断将区间一分为二,并检查中点值的平方与5的接近程度,从而逐步缩小包含根号五的区间,最终得到近似值。
根号五的实际应用
根号五不仅在数学领域有着重要的地位,它在很多实际应用中也发挥着重要作用。以下是一些根号五在不同领域中的应用实例:
几何学与建筑设计:根号五在几何学中有着广泛的应用。例如,在一个正五边形中,每一条对角线的长度与边长的比值就是根号五。这种比例关系使得五边形成为研究对称性和几何变换的一个重要模型。此外,黄金分割比例(约等于1.618)与根号五有直接的关系,它是(1 + 根号五) / 2。黄金分割比例在建筑设计、艺术作品和自然界中广泛存在,因为它被认为是一种视觉上最为和谐的比例。
代数学与二次方程:在代数学中,根号五可以用来解某些二次方程。例如,方程x² - 5 = 0的解就是根号五和负根号五。这说明根号五在解决二次方程问题时具有重要的应用价值。
物理学与工程学:在物理学中,一些公式和理论涉及到根号五的计算。尤其是在涉及到周期性和波动现象的研究中,根号五可能作为系数出现。在工程学中,根号五也可能会出现在计算设计图纸的过程中,尤其是在设计与结构稳定性相关的部分时。
根号五的近似值与精度
根号五的近似值约为2.236,这一数值是数学中常用的估算结果。在实际应用中,我们通常需要根据具体需求来平衡精度与计算成本。对于大多数场景来说,精确到小数点后三位的近似值已经足够满足需求。如果需要更高的精度,可以通过延长迭代次数或使用更精确的计算工具来得到更多位数。然而,需要注意的是,由于无理数的无限不循环特性,我们无法得到一个完全精确的表示。因此,在使用近似值时,需要标注误差范围以确保结果的准确性。
总结
根号五作为一个重要的数学常数,在数学、几何学、代数学、物理学和工程学等多个领域都发挥着重要作用。它表示5的平方根,是一个无理数,其值大约是2.236(无限不循环小数)。根号五的计算方法多种多样,包括牛顿迭代法和二分法等数值方法。在实际应用中,我们需要根据具体需求来选择合适的计算方法和精度范围。通过理解和掌握根号五的性质和应用,我们可以更好地解决各种数学问题,并拓展我们对自然界和艺术中美学比例的理解。
- 上一篇: 揭秘XXS含义:XXS全面翻译解析
- 下一篇: 任末勤学好古:文言文精译与深度注释
-
 揭秘:根号2的精确值究竟是多少?资讯攻略04-27
揭秘:根号2的精确值究竟是多少?资讯攻略04-27 -
 巴西与中国时差到底有多少小时?资讯攻略03-16
巴西与中国时差到底有多少小时?资讯攻略03-16 -
 一标准大气压的具体数值是多少?资讯攻略03-09
一标准大气压的具体数值是多少?资讯攻略03-09 -
 地球表面积的具体数值是多少?资讯攻略03-04
地球表面积的具体数值是多少?资讯攻略03-04 -
 电脑如何打出根号?资讯攻略04-11
电脑如何打出根号?资讯攻略04-11 -
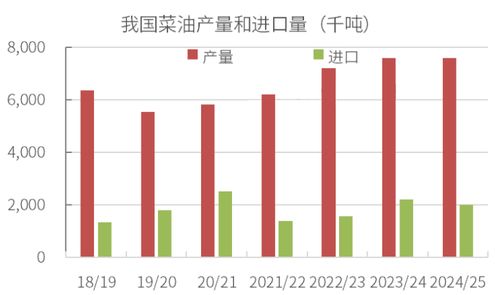 菜籽的出油率是多少?资讯攻略03-01
菜籽的出油率是多少?资讯攻略03-01