指数函数导数:轻松掌握指数函数的求导公式
在数学的浩瀚宇宙中,指数函数如同一颗璀璨的星辰,以其独特的魅力和广泛的应用,引领着无数学子探索的航程。而在探索这条路上,掌握指数函数的导数——这一揭示函数变化速率的神奇钥匙,无疑是每一位数学爱好者必须攀登的高峰。今天,就让我们一同揭开指数函数求导公式的神秘面纱,感受它在数学世界中的无限魅力。
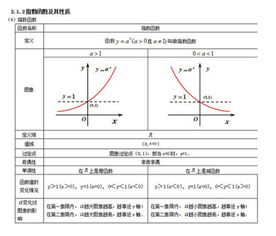
指数函数的奥秘
提及指数函数,我们首先会想到形如y=a^x(a>0且a≠1)的函数表达式。这里,a被称为底数,x为自变量,而y则是因变量。指数函数因其独特的性质,如增长速度随着x的增大而迅速加快,成为了描述自然界中许多增长和衰减现象的理想模型。从细胞分裂到放射性衰变,从人口增长到复利计算,指数函数的身影无处不在。

然而,要深入理解并应用指数函数,仅仅知道它的形式是不够的。我们还需要掌握其导数,即函数值随自变量变化的速度。这不仅是微积分学的基础,也是解决实际问题时不可或缺的工具。

指数函数导数的探索之旅
在数学的探索之旅中,求导就像是打开了一扇通往未知世界的大门。对于指数函数y=a^x而言,其导数是什么呢?
让我们首先回顾一下导数的定义:函数y=f(x)在x=x0处的导数f'(x0),是函数在x0附近变化率的极限值。换句话说,导数描述了函数值随自变量微小变化而变化的快慢程度。
对于指数函数y=a^x,其导数f'(x)可以通过链式法则和指数函数的性质推导出来。这里,我们直接给出其导数公式:
f'(x) = ln(a) * a^x
这个公式告诉我们,指数函数y=a^x的导数仍然是一个指数函数,且其底数与原函数相同,但前面多了一个系数ln(a),即底数a的自然对数。
指数函数求导公式的深度解读
1. 系数的奥秘:在指数函数导数公式中,ln(a)作为系数,起到了至关重要的作用。它不仅决定了导数的正负(当a>1时,ln(a)>0,导数为正;当0
指数函数导数在现实生活中的应用
指数函数导数公式的应用远不止于数学理论本身。在现实生活中,它成为了解决众多实际问题的重要工具。
2. 生物学中的细胞分裂:在生物学中,细胞分裂是一个典型的指数增长过程。利用指数函数及其导数,我们可以预测细胞在一定时间内的数量变化,从而为生物医学研究和疾病治疗提供有力的数学支持。
4. 工程学中的增长与衰减模型:在工程学中,许多现象如机械振动、热传导、电流变化等都表现出指数增长或衰减的特性。通过指数函数导数公式,我们可以建立相应的数学模型,从而实现对这些现象的精确描述和预测。
结语:探索未知,开启智慧之门
让我们带着对数学的热爱和对未知的好奇,继续在数学的世界中遨游吧!相信在未来的日子里,指数函数导数公式将会引领我们走向更加广阔的天地,让我们在探索的征途中不断前行、不断成长。
- 上一篇: NBA附加赛规则是什么?
- 下一篇: 探索“发明”的同义词,一网打尽!
-
 sin(α)cos(α)的公式是什么?资讯攻略02-02
sin(α)cos(α)的公式是什么?资讯攻略02-02 -
 揭秘!如何轻松找到阿里指数查询入口?资讯攻略03-30
揭秘!如何轻松找到阿里指数查询入口?资讯攻略03-30 -
 探索tany的不定积分:解锁函数的奥秘之旅资讯攻略03-15
探索tany的不定积分:解锁函数的奥秘之旅资讯攻略03-15 -
 MATLAB中如何高效求解指数函数资讯攻略03-22
MATLAB中如何高效求解指数函数资讯攻略03-22 -
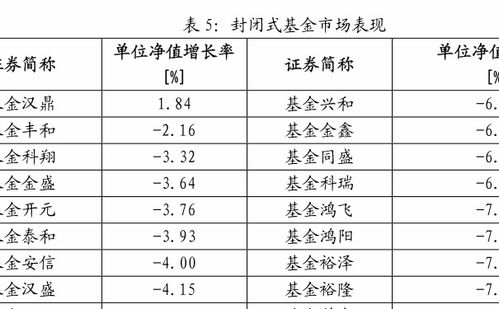 揭秘指数型基金:定义与种类详解资讯攻略04-19
揭秘指数型基金:定义与种类详解资讯攻略04-19 -
 上证380指数的含义资讯攻略03-22
上证380指数的含义资讯攻略03-22