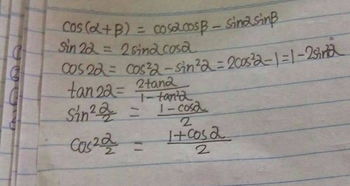探索tany的不定积分:解锁函数的奥秘之旅
探索tany的不定积分:一场数学之旅

在数学的世界里,不定积分如同一座神秘的宝藏,等待着我们去挖掘和探索。今天,让我们携手踏上一段奇妙的旅程,去揭开tany(即tan(y))不定积分的神秘面纱。这不仅是一次对数学公式的简单推导,更是一场关于思维、技巧与数学之美的深度体验。

一、初识tany:三角函数中的舞者
提到tany,我们不禁会想到三角函数这个大家庭。在三角函数的舞台上,tan(y)以其独特的周期性、奇偶性和无穷大特性,成为了一位引人注目的舞者。它的身影在数学、物理乃至工程领域频繁出现,扮演着重要角色。然而,当我们试图求解tany的不定积分时,却会发现这并非一项轻松的任务。

二、挑战与机遇:求解tany的不定积分
求解tany的不定积分,首先面临的是直接积分法的失效。因为tany可以表示为sin(y)/cos(y),而直接对这样的分式进行积分,我们会遇到难以处理的复杂形式。这时,数学中的转换思维显得尤为重要。我们可以尝试将tany转化为其他更容易积分的形式,或者利用三角恒等式进行变形。
方法一:利用三角恒等式进行转换
一个常见的策略是利用三角恒等式sin²(y) + cos²(y) = 1进行转换。我们可以将tany表示为sin(y)/cos(y),然后利用恒等式进行变换,最终得到一个可以积分的形式。但这种方法需要较高的代数技巧和对三角恒等式的深刻理解。
方法二:万能公式法
万能公式法是求解三角函数不定积分的利器。它通过将三角函数表示为tan(y/2)的有理函数,从而简化了积分过程。对于tany,我们可以利用万能公式将其转化为tan(y/2)的有理函数形式,然后利用有理函数的积分方法进行求解。这种方法虽然步骤稍显繁琐,但具有通用性,适用于多种三角函数的不定积分求解。
三、数学之美:探索过程中的发现
在求解tany的不定积分过程中,我们不仅能学到具体的求解技巧,更能深刻体会到数学之美。这种美不仅体现在公式和定理的简洁与优雅上,更体现在解题过程中的思维碰撞和灵感闪现。
1. 思维的灵活性
面对一个看似复杂的问题,我们需要不断调整思路,尝试不同的解题策略。这种思维的灵活性不仅在数学中至关重要,在生活中同样具有重要意义。它教会我们如何在困境中寻找出路,如何灵活应对各种挑战。
2. 细节决定成败
在求解过程中,每一个细节都至关重要。一个微小的错误或遗漏都可能导致整个解题过程的失败。因此,我们需要培养严谨的治学态度,注重每一个步骤的准确性和完整性。
3. 数学与生活的联系
虽然数学看似抽象和枯燥,但它与我们的生活紧密相连。从物理定律到工程设计,从经济分析到计算机科学,数学都扮演着重要角色。通过求解tany的不定积分,我们可以更加深刻地理解数学在现实世界中的应用和价值。
四、实践出真知:动手求解tany的不定积分
现在,让我们动手求解tany的不定积分。以万能公式法为例,我们可以将tany表示为:
tany = 2tan(y/2) / [1 - tan²(y/2)]
然后利用有理函数的积分方法进行求解。虽然过程稍显繁琐,但只要我们耐心细致,一定能够得出正确的结果。
当然,除了万能公式法外,我们还可以尝试其他方法,如利用三角恒等式进行变换、利用部分分式法进行求解等。每一种方法都有其独特的魅力和价值,值得我们深入研究和探索。
五、结语:数学之旅的收获与展望
通过本次对tany不定积分的探索之旅,我们不仅学会了具体的求解技巧和方法,更深刻体会到了数学之美和思维的重要性。这次旅程不仅让我们对数学有了更深入的认识和理解,更为我们未来的学习和生活提供了宝贵的经验和启示。
展望未来,数学的世界依然广阔无垠,等待着我们去继续探索和发现。无论是更高深的数学知识还是更广泛的应用领域,都充满了无限的可能和挑战。让我们保持好奇心和求知欲,勇敢地在数学的海洋中航行吧!
最后,我想说的是,数学不仅仅是一门学科,更是一种思维方式和生活态度。它教会我们如何理性地思考问题、如何严谨地求证答案、如何灵活地应对挑战。在未来的日子里,愿我们都能以数学为伴,共同探索这个充满奥秘和美丽的世界!
- 上一篇: 阿尔卑斯糖背后的深情密语:男孩赠糖的真正含义?
- 下一篇: 常见的浪费水现象有哪些?
-
 探索拼音奥秘:解锁‘排’字的拼音之旅资讯攻略02-14
探索拼音奥秘:解锁‘排’字的拼音之旅资讯攻略02-14 -
 探索“xue”的拼音奥秘:解锁汉语发音新视角资讯攻略02-08
探索“xue”的拼音奥秘:解锁汉语发音新视角资讯攻略02-08 -
 探索UI拼音拼读的全貌:解锁发音奥秘资讯攻略02-05
探索UI拼音拼读的全貌:解锁发音奥秘资讯攻略02-05 -
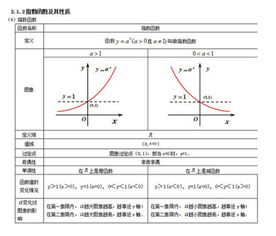 指数函数导数:轻松掌握指数函数的求导公式资讯攻略02-08
指数函数导数:轻松掌握指数函数的求导公式资讯攻略02-08 -
 解锁游戏人生图标,点亮你的游戏之旅!资讯攻略01-05
解锁游戏人生图标,点亮你的游戏之旅!资讯攻略01-05 -
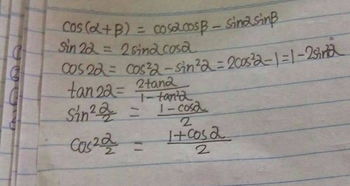 sin(α)cos(α)的公式是什么?资讯攻略02-02
sin(α)cos(α)的公式是什么?资讯攻略02-02