sin(α)cos(α)的公式是什么?
探索sin α cos α的奇妙世界:揭示三角函数中的隐藏宝藏
在数学的海洋中,三角函数如同一颗璀璨的明珠,以其独特的魅力和广泛的应用吸引着无数探索者的目光。而sin α cos α这一组合,更是三角函数世界中的一朵奇葩,它蕴含着丰富的数学关系和实际应用价值。今天,就让我们一同揭开sin α cos α的神秘面纱,探索它背后的奥秘。
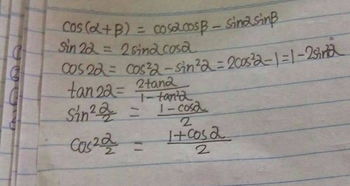
一、sin α cos α的基本关系
在三角函数的基本关系中,sin α和cos α之间存在着一个简单而深刻的联系,即它们的平方和为1。这一关系可以用公式表示为:

(sin α)^2 + (cos α)^2 = 1
虽然这个公式本身并没有直接涉及sin α cos α,但它为推导sin α cos α的相关公式提供了基础。通过一些巧妙的变换,我们可以得到sin α cos α与倍角公式之间的关系。
二、sin α cos α与倍角公式的联系
倍角公式是三角函数中的一个重要工具,它描述了角的二倍与其三角函数值之间的关系。对于正弦函数和余弦函数,倍角公式可以表示为:
sin 2α = 2 sin α cos α
cos 2α = cos^2 α - sin^2 α
这里,sin 2α的表达式直接涉及到了sin α cos α,揭示了这一组合在描述二倍角正弦值时的关键作用。通过这个公式,我们可以轻松地将sin α cos α转化为sin 2α的一半,从而简化计算过程。
三、sin α cos α在实际问题中的应用
sin α cos α不仅在数学理论中具有重要地位,更在实际问题中发挥着不可替代的作用。在工程领域,三角函数被广泛应用于计算角度、距离等参数。而sin α cos α作为正弦和余弦函数的乘积,经常出现在涉及周期性和波动性的问题中。
例如,在描述波动现象时,我们经常会遇到形如A sin(ωt + φ)的波动方程。在这个方程中,A代表振幅,ω代表角频率,t代表时间,φ代表初相位。而sin(ωt + φ)则描述了波动随时间的变化规律。当我们需要计算波动在某个特定时刻的瞬时功率时,sin α cos α的组合就会派上用场。因为瞬时功率与振幅的平方和波动函数的平方成正比,而波动函数的平方可以表示为[sin(ωt + φ)]^2。利用三角恒等变换,我们可以将[sin(ωt + φ)]^2转化为(1/2)[1 - cos(2ωt + 2φ)],进而利用sin α cos α与倍角公式的关系,将其转化为与sin 2α相关的表达式,从而简化计算过程。
此外,在物理学的许多分支中,如力学、电磁学等,sin α cos α也扮演着重要角色。它经常出现在描述物体运动状态、电磁场分布等问题的数学模型中,为科学家和工程师提供了强有力的数学工具。
四、sin α cos α与其他三角函数公式的联系
sin α cos α不仅与倍角公式紧密相连,还与三角函数的其他公式存在着千丝万缕的联系。例如,在和差公式中,我们可以找到sin α cos β和cos α sin β的组合:
sin(α + β) = sin α cos β + cos α sin β
sin(α - β) = sin α cos β - cos α sin β
这些公式描述了两个角的三角函数值如何通过加减运算得到。虽然它们本身并没有直接涉及sin α cos α,但通过一些巧妙的变换和组合,我们可以利用这些公式推导出与sin α cos α相关的新的恒等式和公式。
此外,在积化和差公式和和差化积公式中,我们也可以找到sin α cos α的身影。这些公式将两个三角函数的乘积或和差转化为更简单的形式,从而简化了计算过程。例如,积化和差公式可以将sin α cos β转化为(1/2)[sin(α + β) + sin(α - β)],而和差化积公式则可以将sin α + sin β转化为2 sin[(α + β)/2] cos[(α - β)/2]。
五、sin α cos α的奇妙性质
除了上述的应用和联系外,sin α cos α还具有一些奇妙的性质。例如,它是奇函数和偶函数的乘积。我们知道,sin α是奇函数,即sin(-α) = -sin α;而cos α是偶函数,即cos(-α) = cos α。因此,sin α cos α的奇偶性取决于sin α和cos α的奇偶性组合。由于奇函数乘以偶函数得到的是奇函数,所以sin α cos α也是奇函数,即sin(-α) cos(-α) = -sin α cos α。
此外,sin α cos α还与三角函数的周期性密切相关。我们知道,正弦函数和余弦函数都是周期函数,它们的周期分别为2π和π。而sin α cos α的周期则是这两个周期的最小公倍数,即2π。这意味着sin α cos α的值在每隔2π的区间内会重复出现,呈现出一种周期性的变化规律。
六、结语
综上所述,sin α cos α作为三角函数中的一个重要组合,不仅在数学理论中具有重要地位,更在实际问题中发挥着不可替代的作用。它与倍角公式、和差公式、积化和差公式、和差化积公式等紧密相连,构成了三角函数知识网络中的重要一环。同时,sin α cos α还具有一些奇妙的性质,如奇偶性和周期性等,这些性质使得它在解决特定类型的问题时具有显著的优势。
因此,对于广大数学爱好者和学习者来说,深入理解和掌握sin α cos α的相关知识是至关重要的。通过不断学习和实践,我们可以更好地运用这一组合来解决实际问题,探索数学世界的奥秘。希望本文能够激发你对sin α cos α的兴趣和好奇心,引领你走进三角函数这一神秘而迷人的领域。
- 上一篇: 邓字可以组成哪些词语?
- 下一篇: 急需:嗡字的组词有哪些?
-
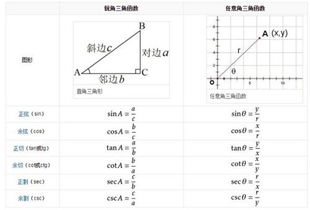 sec(x)的倒数是sin(x)还是cos(x)?资讯攻略04-05
sec(x)的倒数是sin(x)还是cos(x)?资讯攻略04-05 -
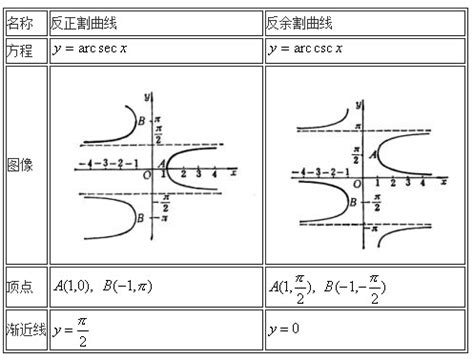 反三角函数的定义域和值域是什么?资讯攻略02-27
反三角函数的定义域和值域是什么?资讯攻略02-27 -
 极化恒等式的定义是什么?资讯攻略04-06
极化恒等式的定义是什么?资讯攻略04-06 -
 《流浪地球》小说终章揭秘资讯攻略02-24
《流浪地球》小说终章揭秘资讯攻略02-24 -
 牛郎星所属星座探究资讯攻略03-18
牛郎星所属星座探究资讯攻略03-18 -
 sin15°的计算结果是多少?资讯攻略02-07
sin15°的计算结果是多少?资讯攻略02-07











