立方根的表达方式或公式是什么?
在数学的浩瀚宇宙中,隐藏着无数令人着迷的公式与定理,它们如同夜空中璀璨的星辰,指引着我们探索未知世界的道路。今天,我们就来揭开一颗特别耀眼的“星辰”——立方根公式的神秘面纱。这不仅是一次对数学知识的深度挖掘,更是一场思维与智慧的奇妙旅行。
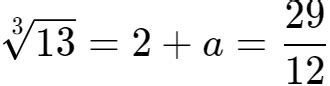
立方根公式的初印象:探索立方与开方的奥秘
想象一下,你手中有一块完美的立方体,无论从哪个方向观察,它的边长都是相等的。现在,如果我们想知道这个立方体的体积是由哪个数的三次方构成的,那么这个问题就涉及到了立方根的概念。简而言之,立方根就是求一个数的立方等于给定数时,这个数是多少。例如,2的立方是8,所以8的立方根就是2。

但数学从不满足于简单的直观理解,它追求的是精准与普适的规律。于是,立方根公式应运而生,它提供了一种求解任意实数立方根的方法,无论是正数、负数还是零,都能在这个公式的框架下找到答案。
立方根公式的真面目:从卡丹公式到简化之路
追溯历史,立方根公式的发现并非一蹴而就。在文艺复兴时期的意大利,数学家尼科洛·丰塔纳(也称为塔尔塔利亚)和杰罗拉莫·卡尔达诺在解决三次方程的过程中,独立或合作地发展出了求解立方根的一般方法,即著名的卡丹公式。这一公式不仅解决了立方方程的求解问题,也为立方根公式奠定了基础。
然而,卡丹公式本身较为复杂,涉及到了平方根、复数以及繁琐的运算步骤。对于普通读者而言,直接应用卡丹公式求解立方根可能显得力不从心。因此,我们需要一个更为简洁直观的立方根公式,或者至少是对卡丹公式的一种简化理解。
简化版立方根公式:实数范围内的直接求解
在实数范围内,我们可以将立方根公式简化为:若a^3 = b,则a = ∛b,这里的“∛”代表立方根符号。这个公式告诉我们,要求b的立方根,只需找到一个数a,使得a的三次方等于b。这种表述虽然直观,但在实际计算中,特别是当b是一个较大的数或者分数时,直接计算可能并不方便。
为了更高效地求解立方根,我们可以借助现代计算器或编程语言的内置函数,这些工具能够迅速给出精确到小数点后多位的立方根值。但如果我们想手动计算,或者想更深入地理解立方根的本质,那么就需要一些技巧和近似方法。
手动计算立方根:逼近法与牛顿迭代法
在没有计算器的情况下,如何手动计算一个数的立方根呢?这里介绍两种常用的方法:逼近法和牛顿迭代法。
逼近法:这种方法基于连续逼近的原理,通过不断调整猜测值来逼近真实的立方根。比如,我们可以从被开方数的某个近似立方根开始,然后计算这个猜测值的立方与被开方数的差值,根据差值的大小和方向来调整猜测值,重复这一过程直到达到所需的精度。
牛顿迭代法:这是一种更为高效的数值求解方法,特别适用于求解方程的根。在求解立方根时,我们可以将问题转化为求解方程x^3 - b = 0的根。牛顿迭代法的核心思想是利用函数的切线来逼近函数的根。具体来说,就是从一个初始猜测值开始,计算函数在该点的导数值(即斜率),然后利用斜率和函数值来构造一个新的猜测值,重复此过程直到收敛到足够精确的解。
立方根公式的应用:从几何到物理的广泛领域
立方根公式不仅在数学领域内占据重要地位,它在几何学、物理学乃至工程学等多个领域都有着广泛的应用。
几何学:在三维空间中,立方体的体积是其边长的三次方。因此,当我们知道立方体的体积时,可以利用立方根公式快速求出其边长。同样地,在求解其他立体图形的体积或表面积时,立方根公式也常常作为辅助工具出现。
物理学:在物理学中,立方根公式与能量、密度、压力等物理量的计算密切相关。例如,在流体力学中,计算管道内流体的流速和压力分布时,可能需要用到立方根来求解相关方程。
工程学:在建筑工程、机械设计等领域,立方根公式同样发挥着重要作用。比如,在设计桥梁、塔楼等结构时,需要精确计算材料的体积和质量分布,以确保结构的稳定性和安全性。此时,立方根公式成为了不可或缺的计算工具。
结语:立方根公式的魅力与启示
通过对立方根公式的探索,我们不难发现,数学不仅仅是数字和符号的堆砌,它更是人类智慧的结晶,是对自然规律和宇宙秩序的深刻洞察。立方根公式作为数学宝库中的一颗璀璨明珠,不仅揭示了立方与开方之间的内在联系,还为我们提供了一种解决复杂问题的新思路和方法。
更重要的是,立方根公式的发现和应用过程,向我们展示了科学探索的艰辛与乐趣。从最初的直观理解到卡丹公式的复杂推导,再到简化版公式的广泛应用,每一步都凝聚着数学家们的智慧与汗水。这一过程告诉我们,科学探索的道路虽然充满挑战,但只要我们坚持不懈、勇于探索,就一定能够发现更多的奥秘和奇迹。
因此,让我们带着对数学的敬畏与热爱,继续在这片充满未知与可能的数学海洋中航行吧!或许下一次,当我们再次仰望星空时,会发现更多的数学星辰在向我们眨眼微笑。
-
 揭秘平方根公式的奥秘资讯攻略02-18
揭秘平方根公式的奥秘资讯攻略02-18 -
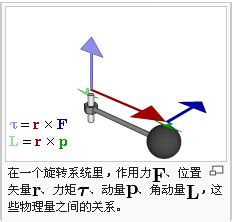 揭秘:力矩的单位究竟是什么?资讯攻略02-19
揭秘:力矩的单位究竟是什么?资讯攻略02-19 -
 电脑如何打出根号?资讯攻略04-11
电脑如何打出根号?资讯攻略04-11 -
 加气砖砌一立方米墙需要多少块砖?资讯攻略02-11
加气砖砌一立方米墙需要多少块砖?资讯攻略02-11 -
 探索动能公式:揭秘物体运动的能量奥秘资讯攻略03-02
探索动能公式:揭秘物体运动的能量奥秘资讯攻略03-02 -
 平面外点到平面距离的计算公式是什么?资讯攻略02-08
平面外点到平面距离的计算公式是什么?资讯攻略02-08












