揭秘平方根公式的奥秘

在我们日常生活中,数学无处不在,从简单的购物计算到复杂的科学研究,都离不开数学的支撑。而在数学的众多领域中,平方根是一个极为基础且重要的概念。那么,平方根公式是什么呢?为什么它如此重要?今天,就让我们一起走进平方根的世界,揭开它的神秘面纱。

首先,我们要明确什么是平方根。平方根,简单来说,就是一个数能被哪个数的平方等于它本身,那么这个数就是那个数的平方根。例如,4的平方根是2,因为2的平方等于4。同样地,-4的平方根是±2,因为2的平方和-2的平方都等于4。但需要注意的是,在实数范围内,我们通常默认非负数的平方根是其正的平方根,即算术平方根。

接下来,我们来看看平方根公式。平方根公式可以表示为:如果一个非负数a的平方等于b,即a²=b,那么a就是b的平方根。为了更直观地理解这个公式,我们可以将其转化为:√b=a(其中b≥0)。这里的√表示平方根符号,它告诉我们要求的是哪个数的平方等于给定的数b。

那么,如何使用这个公式呢?其实,平方根公式在日常生活和科学研究中有着广泛的应用。比如,在物理学中,我们经常需要计算物体的速度、加速度等物理量,而这些物理量的计算往往涉及到平方和平方根运算。在工程学中,平方根公式也用于计算结构的稳定性、材料的强度等关键参数。在金融领域,平方根公式更是被广泛应用于计算复利、评估投资风险等方面。
此外,平方根公式还与许多其他数学概念紧密相连。比如,它与平方、立方等幂运算相互关联,构成了数学运算体系的基础。同时,平方根公式也是解决二次方程、求解不等式等数学问题的重要工具。因此,掌握平方根公式不仅能够帮助我们更好地理解数学,还能让我们在实际应用中更加得心应手。
当然,对于初学者来说,平方根公式可能会显得有些抽象和难以理解。不过,别担心,我们可以通过一些具体的例子来加深理解。
假设我们有一个正方形,它的面积是16平方单位。那么,这个正方形的边长是多少呢?根据平方根公式,我们可以设正方形的边长为a,那么a²就等于正方形的面积,即a²=16。因此,a就是16的平方根,也就是4(在实数范围内,我们只取正值)。所以,这个正方形的边长是4平方单位。
再比如,我们有一个数9,我们想知道哪个数的平方等于9。同样地,我们可以利用平方根公式来求解。设这个数为b,那么b²就等于9。因此,b就是9的平方根,也就是3(同样地,在实数范围内,我们只取正值)。所以,3的平方等于9。
通过这些具体的例子,我们可以发现,平方根公式其实并不神秘,它只是数学运算中的一个基本工具。只要我们理解了它的基本概念和运算规则,就能够轻松地运用它来解决各种问题。
不过,需要注意的是,虽然平方根公式在实数范围内有着广泛的应用,但在某些特定情况下,我们还需要考虑其他类型的平方根。比如,在复数范围内,任何数都有平方根,包括负数和零。此时,平方根公式需要扩展到复数领域,并引入虚数单位i来表示负数的平方根。但是,对于初学者来说,我们主要关注实数范围内的平方根公式及其应用就足够了。
除了基本的平方根公式外,还有一些与之相关的概念和性质也值得我们了解。比如,平方根函数是一个单调递增的函数,这意味着当x的值增大时,√x的值也会相应地增大。同时,平方根函数还具有一些特殊的性质,如:√(ab)=√a×√b(其中a≥0,b≥0),√(a/b)=√a/√b(其中a≥0,b>0)等。这些性质和公式在解决数学问题时非常有用,可以帮助我们简化计算过程并提高工作效率。
总之,平方根公式是数学中的一个基本概念和工具,它广泛应用于各个领域和学科中。掌握平方根公式不仅能够帮助我们更好地理解数学,还能让我们在实际应用中更加得心应手。因此,对于每一个学习数学的人来说,深入了解并熟练掌握平方根公式都是非常重要的。希望通过本文的介绍和解释,你能够对平方根公式有一个更加清晰和深入的认识,并在未来的学习和工作中灵活运用它来解决各种问题。
- 上一篇: 两女一男能否和谐共处
- 下一篇: 揭秘:无产阶级与资产阶级的本质,以及公有制与私有制的奥秘
-
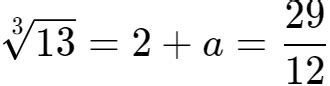 立方根的表达方式或公式是什么?资讯攻略02-18
立方根的表达方式或公式是什么?资讯攻略02-18 -
 揭秘双面胶价格背后的计算奥秘资讯攻略02-15
揭秘双面胶价格背后的计算奥秘资讯攻略02-15 -
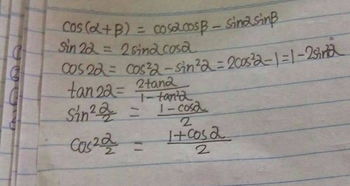 sin(α)cos(α)的公式是什么?资讯攻略02-02
sin(α)cos(α)的公式是什么?资讯攻略02-02 -
 探索动能公式:揭秘物体运动的能量奥秘资讯攻略03-02
探索动能公式:揭秘物体运动的能量奥秘资讯攻略03-02 -
 探索41的平方根:揭秘数学之奥秘资讯攻略03-05
探索41的平方根:揭秘数学之奥秘资讯攻略03-05 -
 揭秘阶乘的神奇计算公式资讯攻略04-05
揭秘阶乘的神奇计算公式资讯攻略04-05