反三角函数的定义域和值域是什么?
在数学的广阔天地里,三角函数是探索角度与边长之间关系的钥匙,而反三角函数,则是打开这扇门的反向途径。它们不像三角函数那样直观易懂,却在解决特定问题时展现出独特的魅力。今天,我们就来一场深入浅出的探索,揭开反三角函数的神秘面纱,特别是它们的定义域和值域,这两大核心特性。
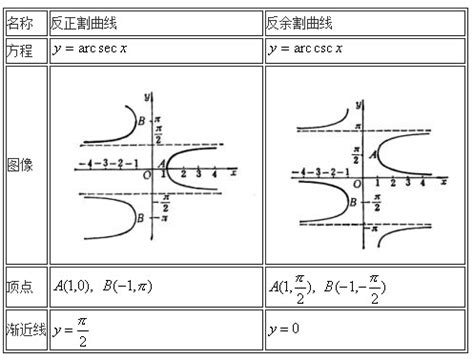
反三角函数的诞生:从“已知角求边”到“已知边求角”
首先,让我们回顾一下三角函数的基础知识。正弦(sin)、余弦(cos)、正切(tan)等函数,是帮助我们根据一个角的大小找到对应的边长比例的。比如,sinθ就是直角三角形中对边与斜边的比值。但现实生活中,我们常常遇到的是已知边长比例,想要知道对应的角度是多少,这时,反三角函数就应运而生了。

反三角函数,顾名思义,就是三角函数的“逆运算”。但需要注意的是,由于三角函数具有周期性(比如sin函数每360度重复一次),反三角函数并不是简单的“一键还原”。为了保持函数的单一性和连续性,数学家们对反三角函数的定义进行了限制,这直接影响了它们的定义域和值域。
正弦函数的反函数:arcsin(反正弦)
定义域与值域揭秘
定义域:arcsin(y)的定义域是[-1, 1]。这是因为正弦函数的值域是[-1, 1],即任何实数角度θ的正弦值都落在这个区间内。为了保持反函数的唯一性,我们只考虑sinθ在这个值域内的角度θ,且限制θ在-π/2到π/2之间(或者说0°到180°的下半部分),这是因为在这个区间内,sinθ是单调递增的。
值域:arcsin(y)的值域是[-π/2, π/2],或者换算成角度就是[-90°, 90°]。这意味着,无论输入y的值是多少(只要y在[-1, 1]内),arcsin(y)给出的结果都是这个区间内的一个角度。
余弦函数的反函数:arccos(反余弦)
定义域与值域探索
定义域:arccos(y)的定义域同样是[-1, 1],理由与arcsin相似,因为余弦函数的值域也是[-1, 1]。为了确保反函数的唯一性,我们考虑cosθ在这个值域内的角度θ,且限制θ在0到π之间(0°到180°),因为在这个区间内,cosθ是单调递减的。
值域:arccos(y)的值域是[0, π],或者说0°到180°。这意味着,无论输入y的值是多少(只要y在[-1, 1]内),arccos(y)给出的结果都是这个区间内的一个角度。
正切函数的反函数:arctan(反正切)
定义域与值域的奥秘
定义域:arctan(x)的定义域是所有实数R,即没有限制。这是因为正切函数的值域是全体实数,无论角度θ取何值,tanθ都可以是任何实数。因此,反正切函数可以接收任何实数值作为输入。
值域:arctan(x)的值域是(-π/2, π/2),或者说-90°到90°之间,但不包括-90°和90°。这是因为在这个区间内,tanθ是单调递增的,且能覆盖所有实数值。尽管正切函数在π/2和-π/2处趋于无穷大,但反正切函数通过限制在这个区间内,保证了输出结果的唯一性和连续性。
小贴士:为何定义域和值域如此重要?
定义域和值域是理解反三角函数的关键。它们不仅决定了函数能够接收哪些输入值,还告诉我们函数将产生哪些输出值。在解决实际问题时,正确识别和使用这些界限至关重要。比如,在物理、工程或计算机图形学中,我们经常需要根据已知的物理量(如力、速度或坐标变换)来求解角度,这时就必须准确运用反三角函数的定义域和值域。
实践中的小技巧
检查输入值:在使用反三角函数之前,先检查输入值是否在函数的定义域内。例如,对于arcsin和arccos,输入值必须在[-1, 1]之间。
理解结果范围:知道反三角函数的值域可以帮助你更好地解释结果。比如,arctan的结果总是介于-90°和90°之间,这有助于你直观地理解角度的大小和方向。
利用计算器:现代计算器提供了方便的反三角函数计算功能,但记得输入值需符合定义域要求,同时理解计算器的输出结果是基于哪个值域的。
结语
反三角函数,虽然不像基本三角函数那样直观,但在解决特定数学和物理问题时发挥着不可替代的作用。通过深入理解它们的定义域和值域,我们不仅能够正确应用这些函数,还能在解决问题的过程中更加游刃有余。下次当你面对一个需要反三角函数来解决的难题时,不妨回想一下这篇文章,让定义域和值域成为你解题路上的得力助手。
- 上一篇: 揭秘:什么是真正的极品?
- 下一篇: 揭秘:有效方法助你结识富有的女性
-
 极化恒等式的定义是什么?资讯攻略04-06
极化恒等式的定义是什么?资讯攻略04-06 -
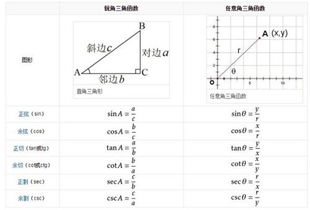 sec(x)的倒数是sin(x)还是cos(x)?资讯攻略04-05
sec(x)的倒数是sin(x)还是cos(x)?资讯攻略04-05 -
 sin15°的计算结果是多少?资讯攻略02-07
sin15°的计算结果是多少?资讯攻略02-07 -
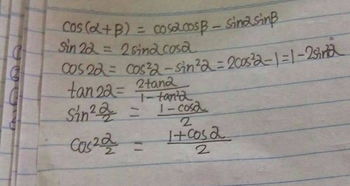 sin(α)cos(α)的公式是什么?资讯攻略02-02
sin(α)cos(α)的公式是什么?资讯攻略02-02 -
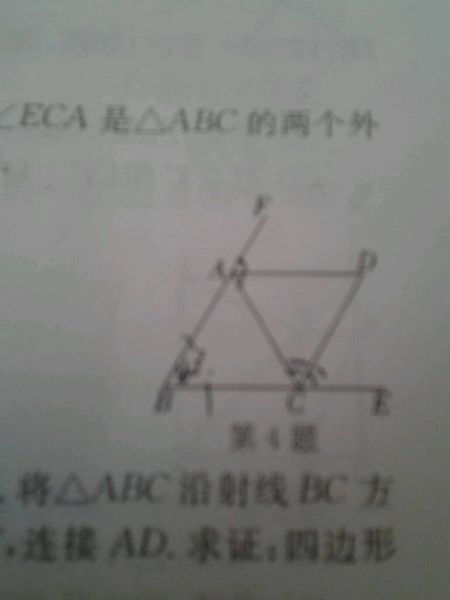 角ABC中,AB等于AC资讯攻略04-12
角ABC中,AB等于AC资讯攻略04-12 -
 数学中IAI的含义是什么资讯攻略03-16
数学中IAI的含义是什么资讯攻略03-16