探索41的平方根:揭秘数学之奥秘
在数学领域中,平方根是一个基础而重要的概念。当我们提到“41的平方根”时,实际上是在寻找一个数,这个数在乘以自己之后等于41。平方根不仅在日常计算中频繁出现,还在几何学、物理学以及工程学等多个学科领域发挥着关键作用。本文将深入探讨41的平方根的概念、计算方法、性质以及在实际应用中的意义。

首先,我们需要明确平方根的定义。一个非负实数a的平方根是指一个数x,使得x的平方等于a。通常,我们将这个数记为√a,读作“a的平方根”。需要注意的是,非负实数都有一个非负的平方根,且唯一确定。然而,对于正实数,除了这个非负的平方根之外,还有一个负的平方根,即-√a,因为(-√a)^2同样等于a。因此,当我们说41的平方根时,实际上有两个数满足条件,即正的平方根和负的平方根。

接下来,我们探讨如何计算41的平方根。对于简单的整数或有限小数,我们可以直接通过试错法或利用已知的平方数进行估算。然而,对于像41这样的非完全平方数,我们无法直接得到一个精确的有限小数或分数作为答案。此时,我们可以借助计算器或数学软件来得到近似值。在常用的科学计算器上,只需输入41,然后按平方根键(√),即可得到近似结果。另外,我们也可以使用数学公式或迭代算法来计算更精确的近似值,但这些方法通常更适合于计算机程序或高级数学学习。

值得注意的是,虽然41的平方根是一个无限不循环小数,但它在数学和科学研究中仍然具有确定的意义和用途。在实际应用中,我们通常会根据需要保留一定数量的小数位,以满足精度要求。例如,在工程设计中,我们可能需要计算某个结构的强度或稳定性,这时就需要用到平方根的概念。即使结果是一个无限不循环小数,我们也可以通过截取有限位来得到一个足够精确的近似值。

除了计算方法之外,41的平方根还具有一些有趣的数学性质。首先,它是一个无理数。无理数是指不能表示为两个整数的比的数,即它们的小数部分是无限不循环的。无理数在数学中占据重要地位,它们与有理数一起构成了实数集。其次,41的平方根与黄金分割率有一定的关联。黄金分割率是一个在自然界和艺术作品中频繁出现的比例关系,它可以用平方根的形式来表示。虽然41的平方根本身并不等于黄金分割率,但通过研究它们之间的关系,我们可以更深入地理解无理数和比例的概念。
此外,41的平方根在几何学中也有应用。例如,在解决与直角三角形相关的问题时,我们可能会用到勾股定理。勾股定理表明,在一个直角三角形中,直角边的平方和等于斜边的平方。如果我们知道直角三角形的两条直角边的长度,就可以利用勾股定理求出斜边的长度;反之亦然。在这个过程中,平方根的概念是必不可少的。虽然41可能不是直角三角形边长的常见值,但了解如何计算任意数的平方根对于理解和应用勾股定理至关重要。
在物理学中,平方根同样扮演着重要角色。例如,在力学中,我们可能会遇到需要计算速度、加速度或力的问题。这些问题往往涉及到距离、时间和质量等物理量的平方或平方根运算。通过利用平方根的概念,我们可以更准确地描述和预测物理现象的变化规律。同样地,在电磁学、热力学等其他物理学分支中,平方根也发挥着类似的作用。
此外,平方根在金融数学和经济学中也有广泛应用。例如,在计算复利、折扣率或股票价格波动时,我们可能会用到平方根的概念。通过利用平方根的性质和运算规则,我们可以更精确地分析金融风险、评估投资收益并制定相应的投资策略。
综上所述,41的平方根虽然是一个看似简单的数学概念,但它在数学、几何学、物理学以及经济学等多个领域都具有广泛的应用和意义。通过深入了解平方根的概念、计算方法和性质,我们可以更好地理解和应用这些领域中的相关知识和技术。同时,我们也应该注意到平方根与无理数、黄金分割率等数学概念之间的紧密联系,这些联系不仅丰富了我们的数学知识体系,也为我们探索自然界和人类社会中的复杂现象提供了有力的工具和方法。
最后需要强调的是,虽然本文主要以41的平方根为例进行介绍和分析,但平方根的概念和性质对于任意正实数都是适用的。因此,在学习和应用平方根时,我们应该注重理解和掌握其基本概念和运算规则,并灵活运用这些知识和技术来解决实际问题。通过不断学习和实践,我们可以逐步提高自己的数学素养和综合能力水平。
- 上一篇: 夏天女性穿丝袜脚臭怎么办?
- 下一篇: 小白兔在恶狼口中的奇遇介绍
-
 揭秘平方根公式的奥秘资讯攻略02-18
揭秘平方根公式的奥秘资讯攻略02-18 -
 立方根的表达方式或公式是什么?资讯攻略02-18
立方根的表达方式或公式是什么?资讯攻略02-18 -
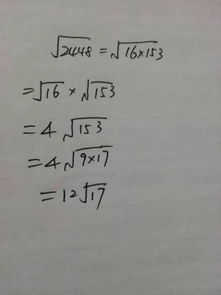 548的算术平方根计算结果是多少?资讯攻略04-06
548的算术平方根计算结果是多少?资讯攻略04-06 -
 探索tany的不定积分:解锁函数的奥秘之旅资讯攻略03-15
探索tany的不定积分:解锁函数的奥秘之旅资讯攻略03-15 -
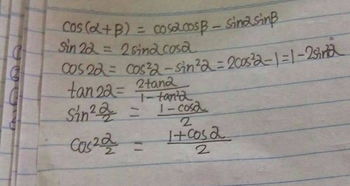 sin(α)cos(α)的公式是什么?资讯攻略02-02
sin(α)cos(α)的公式是什么?资讯攻略02-02 -
 揭秘阶乘的神奇计算公式资讯攻略04-05
揭秘阶乘的神奇计算公式资讯攻略04-05